题目内容
（2010•上饶二模）设函数f(x)=
，若f（4）=f（0），f（2）=-2．则函数F（x）=f（|x|）-|x|的零点个数为（ ）
|
分析：把原函数零点的个数转化为方程的根，进而转化为两个函数图象交点的个数，数形结合，即可求解
解答：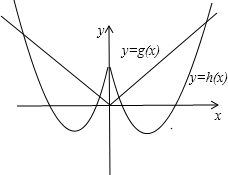
解：∵当x≥0时，f（x）=x2+bx+c，且f（4）=f（0）
∴对称轴为x=-
=2
∴b=-4
又∵f（2）=4-4×2+c=-2
∴c=2
∴当x≥0时，f（x）=x2-4x+2
又函数F（x）=f（|x|）-|x|的零点个数，即为方程F（x）=0的根的个数
即f（|x|）-|x|=0的根的个数
亦即f（|x|）=|x|的根的个数
设h（x）=f（|x|），g（x）=|x|（ ）
原函数零点的个数转化为函数y=h（x），y=g（x）的图象的交点的个数，
y=h（x），y=g（x）图象如图：
有4个不同的交点
故选D
解：∵当x≥0时，f（x）=x2+bx+c，且f（4）=f（0）∴对称轴为x=-
| b |
| 2 |
∴b=-4
又∵f（2）=4-4×2+c=-2
∴c=2
∴当x≥0时，f（x）=x2-4x+2
又函数F（x）=f（|x|）-|x|的零点个数，即为方程F（x）=0的根的个数
即f（|x|）-|x|=0的根的个数
亦即f（|x|）=|x|的根的个数
设h（x）=f（|x|），g（x）=|x|（ ）
原函数零点的个数转化为函数y=h（x），y=g（x）的图象的交点的个数，
y=h（x），y=g（x）图象如图：
有4个不同的交点
故选D
点评：本题考察函数的零点，要注意函数的零点与方程的根，及函数图象与x轴交点的横坐标的关系，同时注意数形结合．作图象时要注意图象变换的方法，如平移变换、伸缩变换、对称变换等
练习册系列答案
优学名师名题系列答案
相关题目