题目内容
【题目】已知椭圆
的离心率为
，且经过点
．
（Ⅰ）求椭圆C的方程；
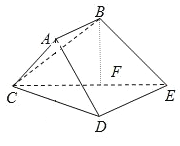
（Ⅱ）过点P（0，2）的直线交椭圆C于A，B两点，求△AOB（O为原点）面积的最大值．
【答案】（Ⅰ）
；（Ⅱ）
.
【解析】试题分析： 
利用
和椭圆经过点
，列方程即可解出
的值，带入即可求得椭圆
的方程
易知斜率存在，设其方程为
，将直线
的方程与椭圆联立，消去
得
，再由根的判别式和韦达定理可求出三角形面积的最大值
解析：（Ⅰ）解：由
，
得
． ①
由椭圆C经过点
，得
． ②…
联立①②，解得 b=1，
．
所以椭圆C的方程是
．
（Ⅱ）易知直线AB的斜率存在，设其方程为y=kx+2．
将直线AB的方程与椭圆C的方程联立，
消去y得 （1+3k2）x2+12kx+9=0．…
令△=144k2﹣36（1+3k2）＞0，得k2＞1．
设A（x1，y1），B（x2，y2），
则
，
． …
所以
． …
因为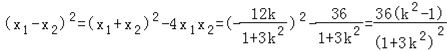
，
设 k2﹣1=t（t＞0），
则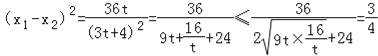
． …
当且仅当
，即
时等号成立，
此时△AOB面积取得最大值
．
练习册系列答案
相关题目
