题目内容
【题目】如图,多面体ABCDE中，四边形ABED是直角梯形，∠BAD=90°，DE∥AB，△ACD是的正三角形，CD=AB=
DE=1，BC=
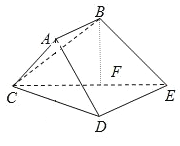
（1）求证：△CDE是直角三角形
（2） F是CE的中点，证明：BF⊥平面CDE
【答案】（1）见解析；（2）见解析
【解析】
(1)根据勾股定理先证明AB⊥AC，结合AB⊥AD，即可证出AB⊥平面ACD，又DE∥AB所以DE⊥平面ACD，即可证明△CDE是直角三角形.
(2) 取CD中点M，连接AM、MF. 先证出MF⊥平面ACD即可得平面CDE⊥平面ACD，利用面面垂直的性质定理可证得AM⊥面CDE，又AM∥BF，即可证出BF⊥平面CDE.
（1）证明：∵∠BAD=90°∴AB⊥AD
△ACD是的正三角形，CD=AB=1，BC=
，
∴△ABC是直角三角形，AB⊥AC
∴AB⊥平面ACD
∵DE∥AB
∴DE⊥平面ACD
∴△CDE是直角三角形
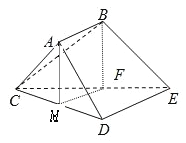
(2)证明:取CD中点M，连接AM、MF.
∵F是CE的中点
∴AMFB是平行四边形
∴MF∥AB，AM∥BF
∴MF⊥平面ACD
∵MF在平面ECD内
∴平面CDE⊥平面ACD
∵△ACD是的正三角形，M是CD中点
∴AM⊥CD
平面CED∩平面ACD=CD,∴AM⊥面CDE，
∵AM∥BF，
∴BF⊥平面CDE
练习册系列答案
名校通行证有效作业系列答案
相关题目
