题目内容
给出命题p：“若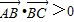
，则△ABC为锐角三角形”；命题q：“实数a，b，c满足b2=ac，则a，b，c成等比数列”，则p∧q为 命题（填“真”或“假”）
【答案】分析：根据向量数量积的定义及向量夹角的定义，可判断命题p的真假；根据等比数列的定义，可判断命题q的真假；进而根据复合命题的真值表，可判断p∧q的真假
解答：解：若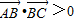
，则cos＜
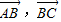＞＞0，此时＜
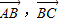＞=π-B为锐角，此时B为钝角，则△ABC为钝角三角形”，故命题p为假命题；
若实数a，b，c满足b2=ac=0，a，b，c不构成等比数列，故命题q为假命题；
故p∧q为假命题
故答案为：假
点评：本题又命题的真假判断为载体，考查了向量的数量积，向量的夹角，等比数列的定义等基本知识点，难度不大，属于基本题型．
解答：解：若
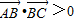，则cos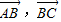＜＞＞0，此时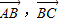＜＞=π-B为锐角，此时B为钝角，则△ABC为钝角三角形”，故命题p为假命题；若实数a，b，c满足b2=ac=0，a，b，c不构成等比数列，故命题q为假命题；
故p∧q为假命题
故答案为：假
点评：本题又命题的真假判断为载体，考查了向量的数量积，向量的夹角，等比数列的定义等基本知识点，难度不大，属于基本题型．
练习册系列答案
相关题目
给出命题p：直线ax+3y+1=0与直线2x+（a+1）y+1=0互相平行的充要条件是a=-3；命题q：若mx2-mx-1＜0恒成立，则-4＜m＜0．关于以上两个命题，下列结论正确的是（ ）
| A、命题“p∧q”为真 | B、命题“p∨q”为假 | C、命题“p∧￢q”为真 | D、命题“p∨￢q”为假 |
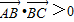，则△ABC为锐角三角形”；命题q：“实数a，b，c满足b2=ac，则a，b，c成等比数列”，则p∧q为 命题（填“真”或“假”）