题目内容
给出命题p:关于x的不等式x2+2x+a>0的解集为R;命题q:函数y=
的定义域为R;若“p∧q”为假命题,“p∨q”为真命题,则a的取值范围是( )
| 1 |
| (x2+a) |
分析:分别求出命题p,q成立的等价条件,然后利用“p∧q”为假命题,“p∨q”为真命题,确定a的取值范围即可.
解答:解:若关于x的不等式x2+2x+a>0的解集为R,
则△=4-4a<0,解得a>1,即p:a>1.
若函数y=
的定义域为R;则x2+a≠0,即a>0,∴q:a>0.
若“p∧q”为假命题,“p∨q”为真命题,
则p,q一真,一假.
若p真,q假,则
,此时a无解.
若p假,q真,则
,解得0<a≤1,
即a的取值范围是(0,1].
故选:D.
则△=4-4a<0,解得a>1,即p:a>1.
若函数y=
| 1 |
| (x2+a) |
若“p∧q”为假命题,“p∨q”为真命题,
则p,q一真,一假.
若p真,q假,则
|
若p假,q真,则
|
即a的取值范围是(0,1].
故选:D.
点评:本题主要考查复合命题与简单命题真假之间的关系的应用,先求出命题p,q成立的等价条件是解决此类问题的关键.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
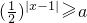 的解集为?,命题q:函数
的解集为?,命题q:函数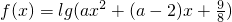 的定义域为R,若命题p和q中有且仅有一个正确,求a的取值范围.
的定义域为R,若命题p和q中有且仅有一个正确,求a的取值范围. 的解集为ϕ,命题q:函数
的解集为ϕ,命题q:函数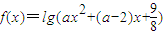 的定义域为R,若命题p和q中有且仅有一个正确,求a的取值范围.
的定义域为R,若命题p和q中有且仅有一个正确,求a的取值范围.