题目内容
【题目】(本小题13分)已知函数f(x)=![]() -
-![]() (a>0,x>0).
(a>0,x>0).
(1)求证:f(x)在(0,+∞)上是单调递增函数;
(2)若f(x)在[![]() ,2]上的值域是[
,2]上的值域是[![]() ,2],求a的值.
,2],求a的值.
【答案】(1)证明:见解析;(2) a=![]() .
.
【解析】本事主要是考查了函数的单调性和函数值域的求解的综合运用。
(1)先分析函数的定义域内任意两个变量,代入函数解析式中作差,然后变形定号,下结论。
(2)∵f(x)在[![]() ,2]上的值域是[
,2]上的值域是[![]() ,2],那么可知又f(x)在[
,2],那么可知又f(x)在[![]() ,2]上单调递增,可知最大值和最小值在端点值取得求解得到参数a的值。
,2]上单调递增,可知最大值和最小值在端点值取得求解得到参数a的值。
解:(1)证明:设x2>x1>0,则x2-x1>0,x1x2>0.
∵f(x2)-f(x1)=(![]() -
-![]() )-(
)-( ![]() -
-![]() )=
)=![]() -
-![]()
=![]() >0,
>0,
∴f(x2)>f(x1),∴f(x)在(0,+∞)上是单调递增的.………………6分
(2)∵f(x)在[![]() ,2]上的值域是[
,2]上的值域是[![]() ,2],
,2],
又f(x)在[![]() ,2]上单调递增,∴f(
,2]上单调递增,∴f(![]() )=
)=![]() ,f(2)=2,
,f(2)=2,
易得a=![]() . ………………13分
. ………………13分

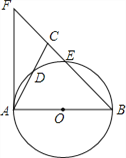
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若![]() ,CE∶EB=1∶4,求CE的长.
,CE∶EB=1∶4,求CE的长.
【题目】某保险公司有一款保险产品的历史收益率(收益率![]() 利润
利润![]() 保费收入)的频率分布直方图如图所示:
保费收入)的频率分布直方图如图所示:
(1)试估计这款保险产品的收益率的平均值;
(2)设每份保单的保费在20元的基础上每增加![]() 元,对应的销量为
元,对应的销量为![]() (万份).从历史销售记录中抽样得到如下5组
(万份).从历史销售记录中抽样得到如下5组![]() 与
与![]() 的对应数据:
的对应数据:
| 25 | 30 | 38 | 45 | 52 |
销量为 | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
由上表,知![]() 与
与![]() 有较强的线性相关关系,且据此计算出的回归方程为
有较强的线性相关关系,且据此计算出的回归方程为![]() .
.

(ⅰ)求参数![]() 的值;
的值;
(ⅱ)若把回归方程![]() 当作
当作![]() 与
与![]() 的线性关系,用(1)中求出的收益率的平均值作为此产品的收益率,试问每份保单的保费定为多少元时此产品可获得最大利润,并求出最大利润.注:保险产品的保费收入
的线性关系,用(1)中求出的收益率的平均值作为此产品的收益率,试问每份保单的保费定为多少元时此产品可获得最大利润,并求出最大利润.注:保险产品的保费收入![]() 每份保单的保费
每份保单的保费![]() 销量.
销量.