题目内容
P是△ABC所在平面外一点,平面α∥平面ABC,α交线段PA.PB.PC于A′.B′.C′,若PA′:AA′=2:3,则△A′B′C′与△ABC的面积比等于
4:25或4:1
4:25或4:1
.分析:由题意推出PA′:PA的值,得到A′B′:AB的值,求出△A′B′C′与△ABC的面积比即可.
解答: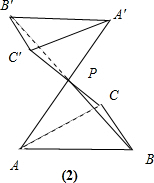
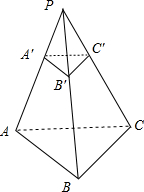 解:由题意画出图形如图:
解:由题意画出图形如图:
因为平面a∥平面ABC,α交线段PA.PB.PC于A′.B′.C′,若PA′:AA′=2:3,
所以A′B′∥AB,
∴△PA′B′∽△PAB
PA′:PA=2:5,A′B′:AB=2:5,
同理A′C′∥AC,A′C′:AC=2:5,
∠B′A′C′=∠BAC.
=
=
=
.同理如图(2)
=4
故答案为:4:25.或4:1

 解:由题意画出图形如图:
解:由题意画出图形如图:因为平面a∥平面ABC,α交线段PA.PB.PC于A′.B′.C′,若PA′:AA′=2:3,
所以A′B′∥AB,
∴△PA′B′∽△PAB
PA′:PA=2:5,A′B′:AB=2:5,
同理A′C′∥AC,A′C′:AC=2:5,
∠B′A′C′=∠BAC.
| S△A′B′C′ |
| S△ABC |
| ||
|
| 2×2 |
| 5×5 |
| 4 |
| 25 |
| S△A′B′C′ |
| S△ABC |
故答案为:4:25.或4:1
点评:本题是基础题,考查几何体的截面面积与底面面积比的求法,考查三角形相似,考查计算能力.

练习册系列答案
相关题目
设P是△ABC所在平面上一点,且
-
=
-
,若△ABC的面积为2,则△PBC面积为( )
| CA |
| CP |
| CP |
| CB |
A、
| ||
| B、1 | ||
| C、2 | ||
| D、4 |