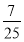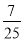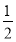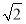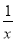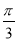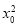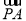题目内容
已知向量a＝
，b＝
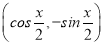，且x∈
.
(1)求a·b及|a＋b|；
(2)若f(x)＝a·b－2λ|a＋b|的最小值为－
，求正实数λ的值．
（1）|a＋b|＝2cosx（2）λ＝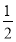
【解析】(1)a·b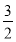＝cos
x·cos
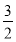－sin
x·sin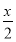
＝cos 2x.
∵a＋b＝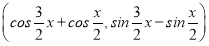
，
∴|a＋b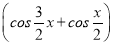|2＝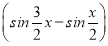
2＋
2
＝2＋2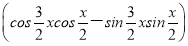
＝2＋2cos 2x＝4cos2x.
∵x∈
，∴cos x≥0.因此|a＋b|＝2cos x.
(2)由(1)知f(x)＝cos 2x－4λcos x＝2cos2x－4λcos x－1，
∴f(x)＝2(cos x－λ)2－1－2λ2，cos x∈[0,1]．
①当0＜λ≤1时，当cos x＝λ时，
f(x)有最小值－1－2λ2＝－
，解得λ＝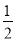
.
②当λ＞1时，当cos x＝1时，f(x)有最小值1－4λ＝－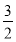
，
λ＝
(舍去)，综上可得λ＝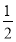
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
