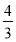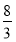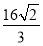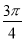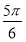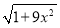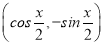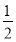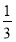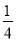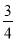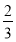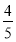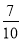题目内容
设点P在曲线y=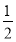 ex上,点Q在曲线y=ln(2x)上,则|PQ|的最小值为( ).
ex上,点Q在曲线y=ln(2x)上,则|PQ|的最小值为( ).
A.1-ln 2 B. (1-ln 2) C.1+ln 2 D.
(1-ln 2) C.1+ln 2 D.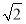 (1+ln 2)
(1+ln 2)
B
【解析】由题意知函数y=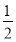 ex与y=ln(2x)互为反函数,其图象关于直线y=x对称,两曲线上点之间的最小距离就是y=x与y=
ex与y=ln(2x)互为反函数,其图象关于直线y=x对称,两曲线上点之间的最小距离就是y=x与y= ex上点的最小距离的2倍.设y=
ex上点的最小距离的2倍.设y=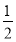 ex上点(x0,y0)处的切线与直线y=x平行.则
ex上点(x0,y0)处的切线与直线y=x平行.则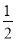 ex0=1,∴x0=ln 2,y0=1,
ex0=1,∴x0=ln 2,y0=1,
∴点(x0,y0)到y=x的距离为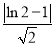 =
=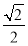 (1-ln 2),
(1-ln 2),
则|PQ|的最小值为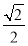 (1-ln 2)×2=
(1-ln 2)×2=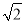 (1-ln 2).
(1-ln 2).

练习册系列答案
相关题目