题目内容
在△ABC中,a,b,c分别是角A,B,C的对边,向量 =(cos
=(cos  ,cos(π-A)-1),
,cos(π-A)-1), =(2cos(
=(2cos( -A),2sin
-A),2sin  ),且
),且 ⊥
⊥
(1)求角A的大小.
(2)设f(x)=cos2x+2sinAsinxcosx,求f(x)的最小正周期,求当 x 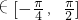 时f(x)的值域.
时f(x)的值域.
解:∵ ⊥
⊥ ,
,
∴ •
• =0,(1分)
=0,(1分)
∴cos •2cos(
•2cos(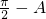 )+[cos(π-A)-1]•2sin
)+[cos(π-A)-1]•2sin =0,(2分)
=0,(2分)
2sinAcos -2cosAsin
-2cosAsin -1=0,(3分)
-1=0,(3分)
2sin(A- )=1,
)=1,
∴sin(A- )=
)= .(4分)
.(4分)
∵0<A<π,
∴- <A-
<A- <
< ,(5分)
,(5分)
∴A- =
=
∴A= ,(6分)
,(6分)
(2)f(x)=cos2x+2sinA•sinxcosx
=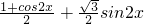 (7分)
(7分)
=sin(2x+ )+
)+ .(8分)
.(8分)
∴T=π,(10分)
∵x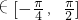 ,
,
∴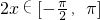 ,
,
∴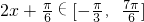 ,
,
∴ ,
,
∴ .(13分)
.(13分)
分析:由 ⊥
⊥ ,知
,知
 =0,所以2sinAcos
=0,所以2sinAcos -2cosAsin
-2cosAsin -1=0,由和(差)角公式得到sin(A-
-1=0,由和(差)角公式得到sin(A- )=
)= ,由此能求出角A的大小.
,由此能求出角A的大小.
(2)先由二倍解公式把f(x)=cos2x+2sinAsinxcosx等价转化为f(x)=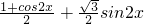 ,再由和(差)角公式进一步转化为f(x)=sin(2x+
,再由和(差)角公式进一步转化为f(x)=sin(2x+ )+
)+ ,由此能求出f(x)的最小正周期和当 x
,由此能求出f(x)的最小正周期和当 x 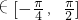 时f(x)的值域.
时f(x)的值域.
点评:本题考查平面向量的综合运用,综合性强,难度大,容易出错.解题时要认真审题,仔细解答,注意二倍角公式、和(差)角公式和三角函数恒等变换的合理运用.
 ⊥
⊥ ,
,∴
 •
• =0,(1分)
=0,(1分)∴cos
 •2cos(
•2cos(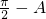 )+[cos(π-A)-1]•2sin
)+[cos(π-A)-1]•2sin =0,(2分)
=0,(2分)2sinAcos
 -2cosAsin
-2cosAsin -1=0,(3分)
-1=0,(3分)2sin(A-
 )=1,
)=1,∴sin(A-
 )=
)= .(4分)
.(4分)∵0<A<π,
∴-
 <A-
<A- <
< ,(5分)
,(5分)∴A-
 =
=
∴A=
 ,(6分)
,(6分)(2)f(x)=cos2x+2sinA•sinxcosx
=
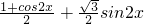 (7分)
(7分)=sin(2x+
 )+
)+ .(8分)
.(8分)∴T=π,(10分)
∵x
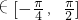 ,
,∴
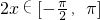 ,
,∴
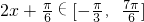 ,
,∴
 ,
,∴
 .(13分)
.(13分)分析:由
 ⊥
⊥ ,知
,知
 =0,所以2sinAcos
=0,所以2sinAcos -2cosAsin
-2cosAsin -1=0,由和(差)角公式得到sin(A-
-1=0,由和(差)角公式得到sin(A- )=
)= ,由此能求出角A的大小.
,由此能求出角A的大小.(2)先由二倍解公式把f(x)=cos2x+2sinAsinxcosx等价转化为f(x)=
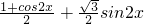 ,再由和(差)角公式进一步转化为f(x)=sin(2x+
,再由和(差)角公式进一步转化为f(x)=sin(2x+ )+
)+ ,由此能求出f(x)的最小正周期和当 x
,由此能求出f(x)的最小正周期和当 x 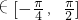 时f(x)的值域.
时f(x)的值域.点评:本题考查平面向量的综合运用,综合性强,难度大,容易出错.解题时要认真审题,仔细解答,注意二倍角公式、和(差)角公式和三角函数恒等变换的合理运用.

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
在△ABC中,∠A、∠B、∠C所对的边长分别是a、b、c.满足2acosC+ccosA=b.则sinA+sinB的最大值是( )
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|