题目内容
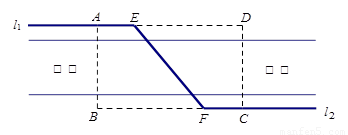
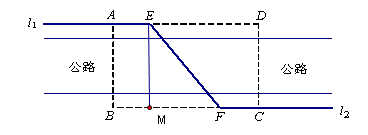
如图,某自来水公司要在公路两侧排水管,公路为东西方向,在路北侧沿直线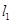 排水管,在路南侧沿直线
排水管,在路南侧沿直线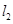 排水管(假设水管与公路的南,北侧在一条直线上且水管的大小看作为一条直线),现要在矩形区域ABCD内沿直线EF将
排水管(假设水管与公路的南,北侧在一条直线上且水管的大小看作为一条直线),现要在矩形区域ABCD内沿直线EF将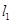 与
与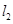 接通.已知AB = 60m,BC = 60
接通.已知AB = 60m,BC = 60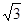 m,公路两侧排管费用为每米1万元,穿过公路的EF部分的排管费用为每米2万元,设EF与AB所成角为
m,公路两侧排管费用为每米1万元,穿过公路的EF部分的排管费用为每米2万元,设EF与AB所成角为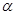 .矩形区域内的排管费用为W.
.矩形区域内的排管费用为W.
(1)求W关于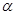 的函数关系式;
的函数关系式;
(2)求W的最小值及相应的角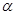 .
.
【答案】
(1)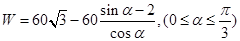 ;(2)
;(2)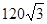 ,
,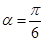 .
.
【解析】
试题分析:(1)过E作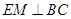 ,垂足为
,垂足为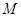 ,然后将
,然后将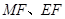 用
用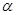 ,再根据题意列出W关于
,再根据题意列出W关于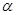 的函数关系式,化简即得
的函数关系式,化简即得 ;(2)设
;(2)设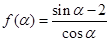 ,
,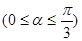 ,再对其求导,通过导函数确定在
,再对其求导,通过导函数确定在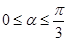 的单调性,从而得到该函数的最大值以及取得最大值时相应的角
的单调性,从而得到该函数的最大值以及取得最大值时相应的角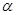 ,代入
,代入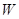 中,即得到W的最小值.
中,即得到W的最小值.
试题解析:(1)如图,过E作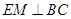 ,垂足为
,垂足为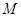 ,由题意得
,由题意得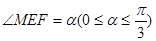 ,
,
故有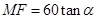 ,
,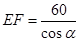 ,
, 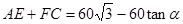 ,
,
所以W= .
.
即 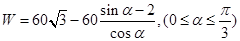 . 6分
. 6分
(2)设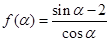 ,
,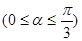
则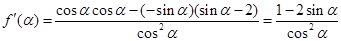 .
.
令 得
得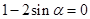 ,即
,即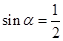 ,得
,得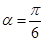 .
.
列表
|
|
|
|
|
|
|
+ |
0 |
- |
|
|
单调递增 |
极大值 |
单调递减 |
所以当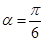 时有
时有 ,此时有.
,此时有.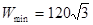
答:排管的最小费用为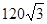 万元,相应的角
万元,相应的角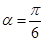 . 13分
. 13分
考点:1.三角函数;2.用导数研究函数的单调性;3.利用单调性求最值.

练习册系列答案
相关题目
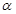
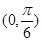
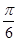
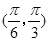
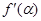
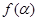
 如图,某自来水公司要在公路两侧排水管,公路为东西方向,在路北侧沿直线排l1,在路南侧沿直线排l2,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB=60m,BC=60
如图,某自来水公司要在公路两侧排水管,公路为东西方向,在路北侧沿直线排l1,在路南侧沿直线排l2,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB=60m,BC=60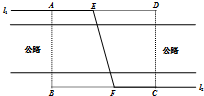 如图,某自来水公司要在公路两侧排水管,公路为东西方向,在路北侧沿直线l1排,在路南侧沿直线l2排,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB=60m,BC=80m,公路两侧排管费用为每米1万元,穿过公路的EF部分的排管费用为每米2万元,设EF与AB所成的小于90°的角为α.
如图,某自来水公司要在公路两侧排水管,公路为东西方向,在路北侧沿直线l1排,在路南侧沿直线l2排,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB=60m,BC=80m,公路两侧排管费用为每米1万元,穿过公路的EF部分的排管费用为每米2万元,设EF与AB所成的小于90°的角为α.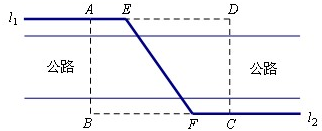

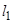 排,在路南侧沿直线
排,在路南侧沿直线 排,现要在矩形区域
排,现要在矩形区域 内沿直线将
内沿直线将 ,
, ,公路两侧排管费用为每米1万元,穿过公路的
,公路两侧排管费用为每米1万元,穿过公路的 部分的排管费用为每米2万元,设
部分的排管费用为每米2万元,设 所成的小于
所成的小于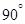 的角为
的角为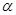 .
.
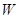 关于
关于