题目内容
 如图,某自来水公司要在公路两侧排水管,公路为东西方向,在路北侧沿直线排l1,在路南侧沿直线排l2,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB=60m,BC=60
如图,某自来水公司要在公路两侧排水管,公路为东西方向,在路北侧沿直线排l1,在路南侧沿直线排l2,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB=60m,BC=60| 3 |
(1)求W关于α的函数关系式;
(2)求W的最小值及相应的角α.
分析:(1)过E作EM⊥BC得到角α,解直角三角形把MF用含α的代数式表示,把AE,FC也用含α的代数式表示,然后即可得到W关于α的函数关系式;
(2)根据导数研究函数最值的方法可求出矩形区域ABCD内的排管费用为W的最小值.
(2)根据导数研究函数最值的方法可求出矩形区域ABCD内的排管费用为W的最小值.
解答:解:(1)如图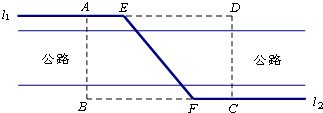 ,
,
过E作EM⊥BC,垂足为M,由题意得∠MEF=α(0≤α≤
),
故有MF=60tanα,EF=
,AE+FC=60
-60tanα,
所以W=(60
-60tanα)×1+
×2=60
-60×
.
(2)设f(α)=
,(0≤α≤
)
则f′(α)=
=
.
令f'(α)=0得1-2sinα=0,即sinα=
,得α=
.
列表
所以当α=
时有f(α)max=-
,此时有.Wmin=120
答:排管的最小费用为120
万元,相应的角α=
.
 ,
,过E作EM⊥BC,垂足为M,由题意得∠MEF=α(0≤α≤
| π |
| 3 |
故有MF=60tanα,EF=
| 60 |
| cosα |
| 3 |
所以W=(60
| 3 |
| 60 |
| cosα |
| 3 |
| sinα-2 |
| cosα |
(2)设f(α)=
| sinα-2 |
| cosα |
| π |
| 3 |
则f′(α)=
| cosαcosα-(-sinα)(sinα-2) |
| cos2α |
| 1-2sinα |
| cos2α |
令f'(α)=0得1-2sinα=0,即sinα=
| 1 |
| 2 |
| π |
| 6 |
列表
| α | (0,
|
|
(
| ||||||||
| f'(α) | + | 0 | - | ||||||||
| f(α) | 单调递增 | 极大值 | 单调递减 |
| π |
| 6 |
| 3 |
| 3 |
答:排管的最小费用为120
| 3 |
| π |
| 6 |
点评:本题考查了根据实际问题选择函数模型,考查了利用导函数求函数的最值,对于实际问题要注意的是需要注明具有实际意义的函数定义域,正确的建模是解答该题的关键,是中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
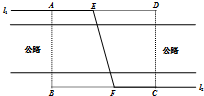 如图,某自来水公司要在公路两侧排水管,公路为东西方向,在路北侧沿直线l1排,在路南侧沿直线l2排,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB=60m,BC=80m,公路两侧排管费用为每米1万元,穿过公路的EF部分的排管费用为每米2万元,设EF与AB所成的小于90°的角为α.
如图,某自来水公司要在公路两侧排水管,公路为东西方向,在路北侧沿直线l1排,在路南侧沿直线l2排,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB=60m,BC=80m,公路两侧排管费用为每米1万元,穿过公路的EF部分的排管费用为每米2万元,设EF与AB所成的小于90°的角为α.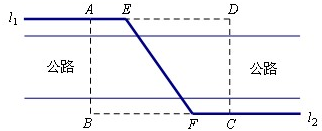

 排,在路南侧沿直线
排,在路南侧沿直线 排,现要在矩形区域
排,现要在矩形区域 内沿直线将
内沿直线将 ,
, ,公路两侧排管费用为每米1万元,穿过公路的
,公路两侧排管费用为每米1万元,穿过公路的 部分的排管费用为每米2万元,设
部分的排管费用为每米2万元,设 所成的小于
所成的小于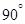 的角为
的角为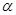 .
.
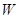 关于
关于