题目内容
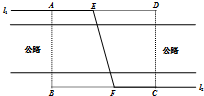 如图,某自来水公司要在公路两侧排水管,公路为东西方向,在路北侧沿直线l1排,在路南侧沿直线l2排,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB=60m,BC=80m,公路两侧排管费用为每米1万元,穿过公路的EF部分的排管费用为每米2万元,设EF与AB所成的小于90°的角为α.
如图,某自来水公司要在公路两侧排水管,公路为东西方向,在路北侧沿直线l1排,在路南侧沿直线l2排,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB=60m,BC=80m,公路两侧排管费用为每米1万元,穿过公路的EF部分的排管费用为每米2万元,设EF与AB所成的小于90°的角为α.(Ⅰ)求矩形区域ABCD内的排管费用W关于α的函数关系;
(Ⅱ)求排管的最小费用及相应的角α.
分析:(Ⅰ)过E作BC的垂线,找出角α,由题意得到角α的范围,用角α表示出公路两侧的长度及公路间的长度,乘以每米的排管费得到函数关系式;
(Ⅱ)引入辅助函数,对函数求导数,利用导数分析最值.
(Ⅱ)引入辅助函数,对函数求导数,利用导数分析最值.
解答:解:(Ⅰ)如图,
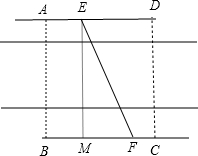
过E作EM⊥BC,垂足为M,由题意得∠MEF=α(0≤tanα≤
).
故有MF=60tanα,EF=
,AE+FC=80-60tanα.
∴W=(80-60tanα)×1+
×2=80-
+
=80-
;
(Ⅱ)设f(α)=
(0≤α≤α0,tanα0=
),
则f′(α)=
=
.
令f′(α)=0,得1-2sinα=0,即sinα=
,得α=
.
∴当α∈(0,
)时,f′(x)>0,f(x)为增函数,
当α∈(
,α0)时,f′(x)<0,f(x)为减函数.
∴当α=
时,有f(α)max=-
,此时Wmin=80+60
.
答:排管的最小费用为80+60
万元,相应的角为α=
.

过E作EM⊥BC,垂足为M,由题意得∠MEF=α(0≤tanα≤
| 4 |
| 3 |
故有MF=60tanα,EF=
| 60 |
| cosα |
∴W=(80-60tanα)×1+
| 60 |
| cosα |
| 60sinα |
| cosα |
| 120 |
| cosα |
| 60(sinα-2) |
| cosα |
(Ⅱ)设f(α)=
| sinα-2 |
| cosα |
| 4 |
| 3 |
则f′(α)=
| cosα•cosα-(-sinα)•(sinα-2) |
| cos2α |
| 1-2sinα |
| cos2α |
令f′(α)=0,得1-2sinα=0,即sinα=
| 1 |
| 2 |
| π |
| 6 |
∴当α∈(0,
| π |
| 6 |
当α∈(
| π |
| 6 |
∴当α=
| π |
| 6 |
| 3 |
| 3 |
答:排管的最小费用为80+60
| 3 |
| π |
| 6 |
点评:本题考查了函数模型的选择及应用,考查了利用导数求闭区间上的最值,把费用正确表示为角α的函数关系是解答该题的关键,是中档题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 如图,某自来水公司要在公路两侧排水管,公路为东西方向,在路北侧沿直线排l1,在路南侧沿直线排l2,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB=60m,BC=60
如图,某自来水公司要在公路两侧排水管,公路为东西方向,在路北侧沿直线排l1,在路南侧沿直线排l2,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB=60m,BC=60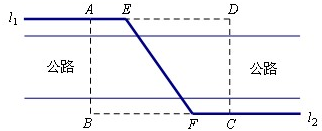

 排,在路南侧沿直线
排,在路南侧沿直线 排,现要在矩形区域
排,现要在矩形区域 内沿直线将
内沿直线将 ,
, ,公路两侧排管费用为每米1万元,穿过公路的
,公路两侧排管费用为每米1万元,穿过公路的 部分的排管费用为每米2万元,设
部分的排管费用为每米2万元,设 所成的小于
所成的小于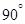 的角为
的角为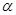 .
.
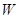 关于
关于