题目内容
10.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>b>0)的右顶点为A,若该双曲线右支上存在两点B,C使得△ABC为等腰直角三角形,则该双曲线的离心率e的取值范围是( )| A. | (1,3) | B. | ($1,\sqrt{3}$) | C. | (1,2) | D. | ($1,\sqrt{2}$) |
分析 设其中一条渐近线与x轴的夹角为θ,由已知条件得tanθ<1,渐近线的方程为$y=\frac{b}{a}x$,从而$\frac{b}{a}<1$,由此能求出该双曲线的离心率e的取值范围.
解答 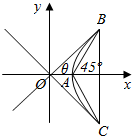 解:如图,因为△ABC为等腰直角三角形,所以∠BAx=45°,
解:如图,因为△ABC为等腰直角三角形,所以∠BAx=45°,
设其中一条渐近线与x轴的夹角为θ,则θ<45°,即tanθ<1,
又上述渐近线的方程为$y=\frac{b}{a}x$,
所以$\frac{b}{a}<1$,又${e^2}=1+\frac{b^2}{a^2}<2$,
所以$1<e<\sqrt{2}$.
故选:D.
点评 本题考查双曲线的离心率的取值范围的求法,是中档题,解题时要认真审题,注意双曲线的性质的合理运用.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
2.设f(x)为定义在R上的奇函数,当x≥0时,有f(x)=$\left\{\begin{array}{l}{log_{\frac{1}{2}}}(x+1),\;x∈[0,1)\\ 1-|x-3|,\;x∈[1,+∞).\end{array}$,则关于x的函数F(x)=f(x)-$\frac{1}{2}$的所有零点之和为( )
| A. | $\sqrt{2}$-1 | B. | $\frac{{\sqrt{2}}}{2}$-1 | C. | 1-$\frac{{\sqrt{2}}}{2}$ | D. | 1-$\sqrt{2}$ |
19.点P是曲线y=x2-1nx上任意一点,则点P到直线y=x-2的距离的最小值是( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
 已知函数f(x)=ax2-|x|+2a-1(a≥1,且a为常数).
已知函数f(x)=ax2-|x|+2a-1(a≥1,且a为常数).