题目内容
16．
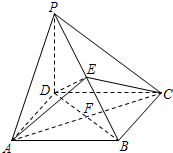如图，在四棱锥P-ABCD中，PD⊥平面ABCD；四边形ABCD是菱形，经过AC作与PD平行的平面交PB与点E，ABCD的两对角线交点为F．求证：AC⊥DE．
分析 连接DE，利用菱形的性质得到AC⊥BD，利用线面垂直的判定定理，只要证明AC⊥平面PBD即可．
解答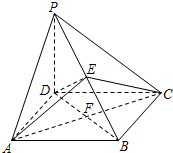 
证明：连接DE．
因为四边形ABCD是菱形，所以AC⊥BD．（4分）
又因为PD⊥平面ABCD，AC?平面ABCD，
所以PD⊥AC．（8分）
而PD∩BD=F，所以AC⊥平面PBD．DE?平面PBD，所以AC⊥DE．（14分）
点评 本题考查了线面垂直的判定定理和性质定理的运用，注意线线垂直与线面垂直的转化．
练习册系列答案
相关题目
8．已知函数f（x）=$\left\{\begin{array}{l}-x+m\\-（m+4）x+{m^2}-m-3\end{array}$$\begin{array}{l}，x≥0\\;x＜0\end{array}$，若对任意的实数x1，x2（x1≠x2）都有$\frac{{f（{x_1}）-f（{x_2}）}}{{{x_1}-{x_2}}}$＜0，则实数m的取值范围是（ ）
| A． | （-4，+∞） | B． | （-∞，-1）∪（3，+∞） | C． | （-∞，-1]∪[3，+∞） | D． | （-4，-1]∪[3，+∞） |
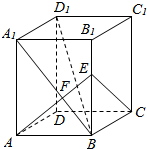如图，已知正四棱柱ABCD-A1B1C1D1 的底面边长为3，侧棱长为4，连接A1B，过A作AF⊥A1B垂足为F，且AF的延长线交B1B于E．