题目内容

20．已知两圆x2+y2=9和（x+4）2+（y+3）2=8，则它们的相交弦长为$\frac{4\sqrt{14}}{5}$．

分析 两圆方程相减，可得公共弦的方程，利用勾股定理，即可求公共弦AB的长．

解答 解：由题意相交弦AB所在的直线方程为：[（x+4）2+（y+3）2-8]-[x2+y2-9]=0，即4x+3y+13=0，
因为圆心（0，0）到直线4x+3y+13=0的距离为$\frac{13}{5}$，所以|AB|=2$\sqrt{9-\frac{169}{25}}$=$\frac{4\sqrt{14}}{5}$．
故答案为：$\frac{4\sqrt{14}}{5}$．

点评 本题考查两圆的位置关系，考查弦长的计算，确定公共弦的方程是关键．

练习册系列答案
相关题目
10．若{1，2}⊆A?{1，2，3，4，5}，则满足条件的集合A的个数为7．
11．若函数f（x）=aln（x+$\sqrt{{x^2}+1}$）+$\frac{b}{{{2^x}-1}}$+$\frac{b+6}{2}$（a，b为常数），在（0，+∞）上有最小值4，则函数f（x）在（-∞，0）上有（　　）
A．最大值4B．最小值-4C．最大值2D．最小值-2
8．方程x2+y2cosα=1，α∈（0，π）表示的曲线不可能是（　　）
A．圆B．椭圆C．双曲线D．直线
15．已知函数f（x）=x3+ax2+bx+c （a，b，c∈R）在x=-1处有极值，在x=3处的切线方程为y=-16．
（1）求a，b，c的值；
（2）求函数f（x）在[-3，4]上的最大值与最小值．
5．已知记号max{a，b}=$\left\{\begin{array}{l}{a；a≥b}\\{b；a＜b}\end{array}\right.$，f（x）=max{tanπx，sinπx}，则直线y=$\frac{1}{2}$与g（x）=|f（x）cosπx|的图象在区间[0，n]，n∈N*内交点的横坐标之和记为Sn，则Sn=n2-$\frac{n}{12}$．
12．观察式子：
cos$\frac{2}{3}$π=-$\frac{1}{2}$；
cos$\frac{2}{5}$π+cos$\frac{4}{5}$π=-$\frac{1}{2}$；
cos$\frac{2}{7}$π+cos$\frac{4}{7}$π+cos$\frac{6}{7}$π=-$\frac{1}{2}$；
按此规律猜想第五个的等式为cos$\frac{2}{11}$π+cos$\frac{4}{11}$π+cos$\frac{6}{11}$π+cos$\frac{8}{11}$π+cos$\frac{10}{11}$π=-$\frac{1}{2}$．
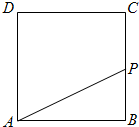9．如图所示，在边长为4的正方形ABCD的边上有一点P，当P点由点B（起点）向点A（终点）沿逆时针方向移动（B→C→D→A）时，三点A、B、P构成△ABP，求：
（1）△ABP的面积y关于点P移动的路程x的函数关系式；
（2）当路程x为多少时面积y有最大值？并求此最大值．
10．已知A（-1，3），B（1，1），C（x，y）．
（1）若A，B，C三点共线，求x与y的关系式；
（2）若$\overrightarrow{AC}$=2$\overrightarrow{AB}$，求点C的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网