题目内容
【题目】已知函数![]() .
.
(1)求函数![]() 的极值;
的极值;
(2)若对于任意的![]() ,若函数
,若函数![]() 在区间
在区间![]() 上有最值,求实数
上有最值,求实数![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,
时, ![]() 无极值,当
无极值,当![]() 时,
时, ![]() 有极大值
有极大值![]() ,无极小值;(2)
,无极小值;(2)![]() .
.
【解析】试题分析:(1)对![]() 求导,
求导, ![]() ,分
,分![]() ,
, ![]() 两种情况写出函数的单调区间;(2)对函数
两种情况写出函数的单调区间;(2)对函数![]() 求导得
求导得![]() ,根据
,根据![]() 在区间
在区间![]() 上有最值,得到
上有最值,得到![]() 在区间
在区间![]() 上总不是单调函数,从而得到
上总不是单调函数,从而得到![]() ,∴
,∴ ,另由对任意
,另由对任意![]() ,
, ![]() 恒成立,分离参数即可求得实数
恒成立,分离参数即可求得实数![]() 的取值范围.
的取值范围.
试题解析:(1)由已知得![]() 的定义域为
的定义域为![]() ,且
,且![]() ,
,
当![]() 时,
时, ![]() ,
,
∴![]() 在
在![]() 单调增,
单调增, ![]() 无极值;
无极值;
当![]() 时,
时,
由![]() 得:
得: ![]() ,则
,则![]() 得:
得: ![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
∴![]() 的极大值
的极大值![]() ,无极小值.
,无极小值.
综上:当![]() 时,
时, ![]() 无极值;
无极值;
当![]() 时,
时, ![]() 有极大值
有极大值![]() ,无极小值.
,无极小值.
(2)![]() ,
,
∴![]() ,
,
∵![]() 在区间
在区间![]() 上有最值,
上有最值,
∴![]() 在区间
在区间![]() 上有极值,即方程
上有极值,即方程![]() 在
在![]() 上有一个或两个不等实根,
上有一个或两个不等实根,
又![]() ,∴
,∴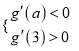
则题意知:对任意![]() ,
, ![]() 恒成立,
恒成立,
∴![]() ,因为
,因为![]() ,∴
,∴![]() ,
,
对任意![]() ,
, ![]() 恒成立
恒成立
∴![]() ,∵
,∵![]() ,∴
,∴![]()
∴![]() .
.

 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ),以原点
),以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 与
与![]() 的直角坐标方程;
的直角坐标方程;
(2)当![]() 与
与![]() 有两个公共点时,求实数
有两个公共点时,求实数![]() 的取值范围.
的取值范围.
【题目】电视传媒公司为了解某地区观众对某体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名,下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
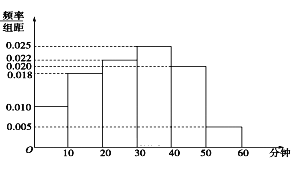
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.
(1)根据已知条件完成下面的22列联表,并据此资料你是否认为“体育迷”与性别有关?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
(2)将上述调查所得到的频率视为概率.现在从该地区大量电视观众中,采用随机抽样方法每次抽取1名观众,抽取3次,记被抽取的3名观众中的“体育迷”人数为X.若每次抽取的结果是相互独立的,求X的分布列,期望E(X)和方差D(X).
附:![]() .
.
P(K2≥k) | 0.05 | 0.01 |
k | 3.841 | 6.635 |