题目内容
9.若定义在R上的函数f(x)满足f(0)=-1,其导函数f′(x)满足f′(x)>k>1,则下列结论中一定错误的是( )| A. | $f({\frac{1}{k}})<\frac{1}{k}$ | B. | $f({\frac{1}{k}})>\frac{1}{k-1}$ | C. | $f({\frac{1}{k-1}})<\frac{1}{k-1}$ | D. | $f({\frac{1}{k-1}})>\frac{k}{k-1}$ |
分析 根据导数的概念得出$\frac{f(x)-f(0)}{x}$>k>1,用x=$\frac{1}{k-1}$代入可判断出f($\frac{1}{k-1}$)>$\frac{1}{k-1}$,即可判断答案.
解答 解;∵f′(0)=$\underset{lim}{x→0}$$\frac{f(x)-f(0)}{x-0}$
f′(x)>k>1,
∴$\frac{f(x)-f(0)}{x}$>k>1,
即$\frac{f(x)+1}{x}$>k>1,
当x=$\frac{1}{k-1}$时,f($\frac{1}{k-1}$)+1>$\frac{1}{k-1}$×k=$\frac{k}{k-1}$,
即f($\frac{1}{k-1}$)$>\frac{k}{k-1}$-1=$\frac{1}{k-1}$
故f($\frac{1}{k-1}$)>$\frac{1}{k-1}$,
所以f($\frac{1}{k-1}$)<$\frac{1}{k-1}$,一定出错,
另解:设g(x)=f(x)-kx+1,
g(0)=0,且g′(x)=f′(x)-k>0,
g(x)在R上递增,
k>1,对选项一一判断,可得C错.
故选:C.
点评 本题考查了导数的概念,不等式的化简运算,属于中档题,理解了变量的代换问题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目
19.若tanα=$\frac{1}{3}$,tan(α+β)=$\frac{1}{2}$,则tanβ=( )
| A. | $\frac{1}{7}$ | B. | $\frac{1}{6}$ | C. | $\frac{5}{7}$ | D. | $\frac{5}{6}$ |
20.若集合M={x|-2≤x<2},N={0,1,2},则M∩N=( )
| A. | {0} | B. | {1} | C. | {0,1,2} | D. | {0,1} |
4.若变量x,y满足约束条件$\left\{\begin{array}{l}x+2y≥0\\ x-y≤0\\ x-2y+2≥0\end{array}\right.$则z=2x-y的最小值等于( )
| A. | $-\frac{5}{2}$ | B. | -2 | C. | $-\frac{3}{2}$ | D. | 2 |
18.阅读如图所示的程序框图,运行相应的程序,则输出i的值为( )
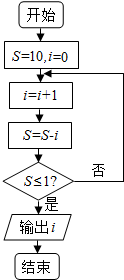

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
9.已知A,B分别为椭圆$\frac{x{\;}^{2}}{a{\;}^{2}}$+$\frac{y{\;}^{2}}{b{\;}^{2}}$=1(a>b>0)的右顶点和上顶点,直线y=kx(k>0)与椭圆交于C,D两点,若四边形ABCD的面积最大值为2c2,则椭圆的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{2}}{2}$ |
 如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1,
如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1,