题目内容
(本小题满分12分)
如图,在四边形ABCD中,AC平分∠DAB,∠ABC=600,AC=7,AD=6,S△ADC= ,
,
求AB的长.
8
解析试题分析:在△ADC中,已知AC=7,AD=6,S△ADC= ,则由S△ADC=
,则由S△ADC=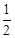 •AC•AD•sin∠DAC,
•AC•AD•sin∠DAC,
∴sin∠DAC=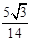 ,又AC为∠DAB的平分线,∠1+∠2<180°得∠BAC=∠DAC为锐角,∴cos∠2 =
,又AC为∠DAB的平分线,∠1+∠2<180°得∠BAC=∠DAC为锐角,∴cos∠2 =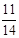 ,∴∠ACB=120°-∠2,∴sin∠ACB=sin(120°-∠2)= sin120°cos∠2- cos120°sin∠2)=
,∴∠ACB=120°-∠2,∴sin∠ACB=sin(120°-∠2)= sin120°cos∠2- cos120°sin∠2)=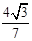 ,又AC=7,∴由正弦定理
,又AC=7,∴由正弦定理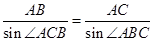 得:AB=
得:AB=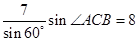
考点:本题考查了正余弦定理的运用
点评:解三角形的内容不仅能考查正、余弦定理的应用,而且能很好地考查三角变换的技巧,它还可与立体几何、解析几何、向量、数列、概率等知识相结合,这其中经常涉及到数形结合、分类讨论及等价转化等思想方法.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
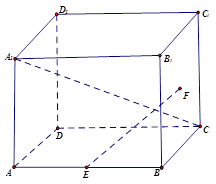
 中,四边形
中,四边形 是菱形,
是菱形,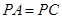 ,
, 为
为 的中点.
的中点.
 面
面 ; (2)求证:平面
; (2)求证:平面 平面
平面 .
. 的底面
的底面 为平行四边形,
为平行四边形, 分别是棱
分别是棱 的中点,平面
的中点,平面 与平面
与平面 交于
交于 ,求证:
,求证:
 平面
平面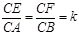 ,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).
,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2). 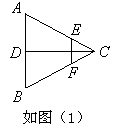
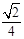 ,求k的值.
,求k的值.  ⊥平面
⊥平面 ,
, ,
, ,
, ,
, ,
, ,
, ,
,  是
是 的中点.
的中点.
 平面
平面 ;
; ;
;
 、
、 分别是
分别是 、
、 的中点,
的中点, 是
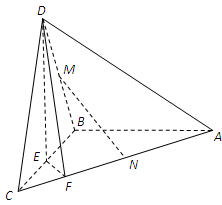
是 上的一动点,主视图与俯视图都为正方形。
上的一动点,主视图与俯视图都为正方形。

 ;
; 时,在棱
时,在棱 上确定一点
上确定一点 ,使得
,使得 ∥平面
∥平面 ,并给出证明。
,并给出证明。 的平面角余弦值。
的平面角余弦值。