题目内容
如图,正方体ABCD—A1B1C1D1中,E为AB中点,F为正方形BCC1B1的中心.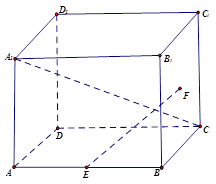
(1)求直线EF与平面ABCD所成角的正切值;
(2)求异面直线A1C与EF所成角的余弦值.
(1)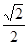 (2)
(2)
解析试题分析:解法一:(1)取BC中点H,连结FH,EH,设正方体棱长为2.
∵F为BCC1B1中心,E为AB中点.
∴FH⊥平面ABCD,FH=1,EH=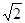 .
.
∴∠FEH为直线EF与平面ABCD所成角,且FH⊥EH.
∴tan∠FEH=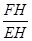 =
=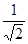 =
=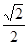 .……6分
.……6分
(2)取A1C中点O,连接OF,OA,则OF∥AE,且OF=AE.
∴四边形AEFO为平行四边形.∴AO∥EF.
∴∠AOA1为异面直线A1C与EF所成角.
∵A1A=2,AO=A1O=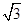 .
.
∴△AOA1中,由余弦定理得cos∠A1OA= .……12分
.……12分
解法二:设正方体棱长为2,以B为原点,BC为x轴,BA为y轴,BB1为z轴,建立空间直角坐标系.则B(0,0,0),B1(0,0,2),E(0,1,0),F(1,0,1),
C(2,0,0),A1(0,2,2).
(1)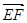 =(1,-1,1),
=(1,-1,1),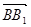 =(0,0,2),且
=(0,0,2),且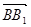 为平面ABCD的法向量.
为平面ABCD的法向量.
∴cos<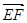 ,
,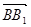 >=
>= .
.
设直线EF与平面ABCD所成角大小为θ.
∴sinθ= ,从而tanθ=
,从而tanθ=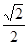 .……6分
.……6分
(2)∵ =(2,-2,-2).∴cos<
=(2,-2,-2).∴cos<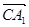 ,
,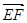 >=
>= .
.
∴异面直线A1C与EF所成角的余弦值为 .……12分
.……12分
考点:异面直线所成的角,线面角
点评:解决的关键是根据异面直线所成角的定义, 以及线面角的概念,结合向量法来得到,属于基础题。

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
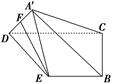
 棱长为1,
棱长为1, 是
是 的中点,
的中点, 是
是 的中点.
的中点. 
 ;
; 的余弦值.
的余弦值. ,在直线DE上是否存在一点
,在直线DE上是否存在一点 ,使得
,使得 ∥面BCD?若存在,请指出点
∥面BCD?若存在,请指出点

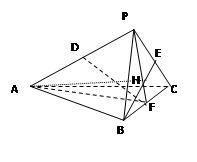
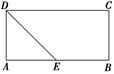
 平面ABCD,EF∥AB, AB=2EF=2AD=4,
平面ABCD,EF∥AB, AB=2EF=2AD=4, .
.
 ,如图二,在二面角
,如图二,在二面角
 的所有棱长都为2,
的所有棱长都为2, 为
为 中点,
中点, 平面
平面

 平面
平面 ;
; 的余弦值;
的余弦值; 到平面
到平面 ,
,