题目内容
6.已知点P为曲线xy-2x-2y+8=0上任意一点,O为坐标原点,则|OP|的最小值为$\frac{\sqrt{6}}{3}$.分析 根据两点间的距离公式,利用配方法进行转化即可得到结论.
解答 解:设P(x,y),
则|OP|=$\sqrt{{x}^{2}+{y}^{2}}$=$\sqrt{{x}^{2}+{y}^{2}+xy-2x-2y+8}$=$\sqrt{\frac{3}{4}(x-\frac{2}{3})^{2}+(\frac{1}{2}x+y-1)^{2}+\frac{2}{3}}$≥$\frac{\sqrt{6}}{3}$,
当且仅当x=$\frac{2}{3}$,y=$\frac{2}{3}$取等号,
故|OP|的最小值是$\frac{\sqrt{6}}{3}$,
故答案为:$\frac{\sqrt{6}}{3}$.
点评 本题主要考查两点间的距离的求解,利用配方法将式子进行配方是解决本题的关键.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案
相关题目
16.在△ABC中,a、b、c分别为角A、B、C的对边,若∠B=$\frac{π}{6}$,b=1,c=2,则a=( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{7}$ |
14.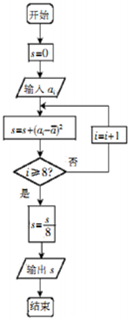 如图是一个算法的程序框图(其中$\overline{a}$是这8个数据的平均数),若输入ai的值如下表,则输出s的值是( )
如图是一个算法的程序框图(其中$\overline{a}$是这8个数据的平均数),若输入ai的值如下表,则输出s的值是( )
 如图是一个算法的程序框图(其中$\overline{a}$是这8个数据的平均数),若输入ai的值如下表,则输出s的值是( )
如图是一个算法的程序框图(其中$\overline{a}$是这8个数据的平均数),若输入ai的值如下表,则输出s的值是( )| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 |
| 39 | 40 | 42 | 42 | 43 | 45 | 46 | 47 |
| A. | A | B. | B | C. | C | D. | D |
11.执行如图所示的程序框图,如果输出i=4,那么空白的判断框中应填入的条件是( )
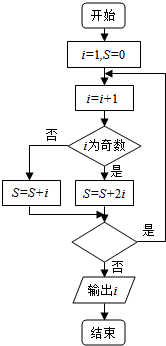

| A. | S≤10? | B. | S≤12? | C. | S≤14? | D. | S≤16? |