题目内容
1.已知数列{an}满足an+1=a${\;}_{n}^{2}$-nan+1,且a1=2.(1)计算a2,a3,a4的值,由此猜想数列{an}的通项公式,并用数学归纳法证明;
(2)求证:2nn≤a${\;}_{n}^{n}$<3nn.
分析 (1)由an+1=a${\;}_{n}^{2}$-nan+1,且a1=2,分别令 n=2,3,4即可求解,进而可猜想,然后利用数学归纳法进行证明即可;
(2)由(1)可得an=n+1,从而有${{a}_{n}}^{n}$=(n+1)n,利用二项式定理展开式以及构造函数,利用单调性证明.
解答 解:(1)由已知an+1=a${\;}_{n}^{2}$-nan+1,且a1=2.得到a2=${{a}_{1}}^{2}$-a1+1=3,a3=${{a}_{2}}^{2}$-2a2+1=4,a4=${{a}_{3}}^{2}$-3a3+1=5;
由此猜测数列{an}的通项公式为an=n+1;
证明:①n=1,2,3,4显然成立;
②假设n=k时成立,即ak=k+1,则n=k+1时,ak+1=${{a}_{k}}^{2}$-kak+1=(k+1)2-k(k+1)+1=k+2=(k+1)+1;
所以n=k+1时,数列an=n+1也成立;
所以数列{an}的通项公式an=n+1对任意n∈N+都成立;
(2)因为an=n+1,所以${{a}_{n}}^{n}$=(n+1)n=${C}_{n}^{0}{n}^{n}+{C}_{n}^{1}{n}^{n-1}+{C}_{n}^{2}{n}^{n-2}+…{C}_{n}^{n}$>${C}_{n}^{0}{n}^{n}+{C}_{n}^{1}{n}^{n-1}$=2nn;
构造函数f(x)=(1+$\frac{1}{x}$)x,则f′(x)=(1+$\frac{1}{x}$)xln(1+$\frac{1}{x}$)(-$\frac{1}{{x}^{2}}$)<0,所以函数f(x)为减函数,又x≥1,所以f(x)≤f(1)=2<3,所以$(\frac{n+1}{n})^{n}$=$(1+\frac{1}{n})^{n}$<3,
即(n+1)n<3nn;
所以2nn≤a${\;}_{n}^{n}$<3nn.
点评 本题主要考查了数列的递推公式在求解数列的通项综合的应用及归纳法的应用,解答(2)左边的关键是二项展开式的应用,右边是构造函数法.

 名校课堂系列答案
名校课堂系列答案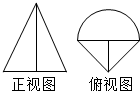 由两个简单几何体构成的组合几何体的三视图中,正视图和俯视图如右图所示,其中正视图中等腰三角形的高为3,俯视图中的三角形均为等腰直角三角形,半圆直径为2,则该几何体的体积为( )
由两个简单几何体构成的组合几何体的三视图中,正视图和俯视图如右图所示,其中正视图中等腰三角形的高为3,俯视图中的三角形均为等腰直角三角形,半圆直径为2,则该几何体的体积为( )| A. | $\frac{π}{2}+1$ | B. | π+1 | C. | $\frac{π}{2}+2$ | D. | π+2 |