题目内容
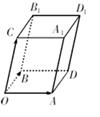
如图所示,正方体ABCD-A1B1C1D1,M为AA1的中点,N为A1B1上的点,且满足 A1N=
A1N= NB1,P为底面正方形A1B1C1D1的中心.求证:MN⊥MC,MP⊥B1C.
NB1,P为底面正方形A1B1C1D1的中心.求证:MN⊥MC,MP⊥B1C.
 A1N=
A1N= NB1,P为底面正方形A1B1C1D1的中心.求证:MN⊥MC,MP⊥B1C.
NB1,P为底面正方形A1B1C1D1的中心.求证:MN⊥MC,MP⊥B1C.证明略
设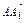 =a,
=a,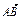 =b,
=b,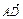 =c
=c
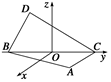
则a、b、c两两垂直且模相等.
∴a·b=b·c=a·c=0,
又∵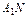 =
= NB1
NB1
∴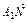 =
=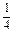
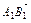 =
=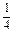 b,
b,
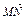 =
=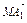 +
+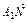 =
=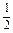 a+
a+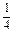 b,
b,
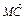 =
=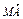 +
+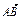 +
+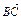 =-
=-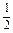 a+b+c,
a+b+c,
∴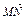 ·
·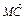 =(
=(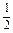 a+
a+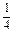 b)·(b+c-
b)·(b+c-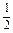 a)
a)
=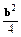 -
-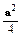 =0.
=0.
∴MN⊥MC,
又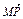 =
=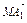 +
+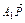 =
=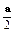 +
+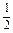 (b+c)=
(b+c)=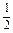 (a+b+c),
(a+b+c),
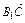 =
=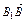 +
+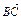 =-a+c.
=-a+c.
∴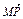 ·
·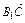 =
=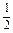 (a+b+c)(c-a)=0.∴MP⊥B1C.
(a+b+c)(c-a)=0.∴MP⊥B1C.
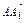 =a,
=a,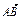 =b,
=b,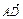 =c
=c
则a、b、c两两垂直且模相等.
∴a·b=b·c=a·c=0,
又∵
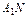 =
= NB1
NB1∴
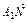 =
=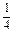
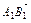 =
=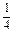 b,
b,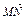 =
=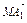 +
+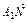 =
=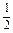 a+
a+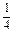 b,
b,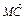 =
=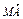 +
+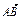 +
+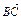 =-
=-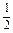 a+b+c,
a+b+c,∴
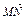 ·
·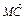 =(
=(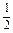 a+
a+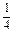 b)·(b+c-
b)·(b+c-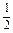 a)
a)=
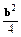 -
-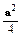 =0.
=0.∴MN⊥MC,
又
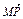 =
=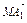 +
+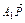 =
=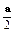 +
+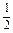 (b+c)=
(b+c)=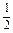 (a+b+c),
(a+b+c),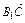 =
=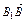 +
+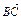 =-a+c.
=-a+c.∴
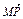 ·
·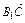 =
=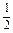 (a+b+c)(c-a)=0.∴MP⊥B1C.
(a+b+c)(c-a)=0.∴MP⊥B1C.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
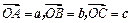 ,可构成空间向量的一个基底,若
,可构成空间向量的一个基底,若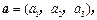
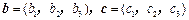 ,在向量已有的运算法则的基础上,新定义一种运算
,在向量已有的运算法则的基础上,新定义一种运算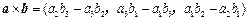 ,显然
,显然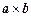 的结果仍为一向量,记作
的结果仍为一向量,记作 .
.
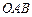 的法向量;
的法向量;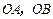 为边的平行四边形
为边的平行四边形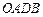 的面积等于
的面积等于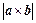 ;
;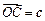 平移,得到一个平行六面体
平移,得到一个平行六面体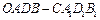 ,试判断平行六面体的体积
,试判断平行六面体的体积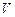 与
与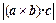 的大小.
的大小.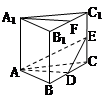
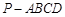 ,底面
,底面 为矩形,侧棱
为矩形,侧棱 ,其中
,其中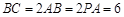 ,
,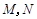 为侧棱
为侧棱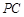 上的两个三等分点,如下图所示.
上的两个三等分点,如下图所示.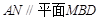 ;
;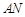 与
与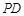 所成角的余弦值;
所成角的余弦值;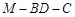 的余弦值.
的余弦值.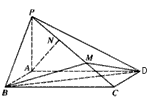
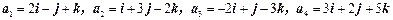 ,试问是否存在实数
,试问是否存在实数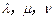 ,使
,使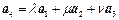 成立?如果存在,求出
成立?如果存在,求出
 中,若
中,若 则
则 ( )
( )


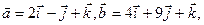 ,则这两个向量的位置关系是___________。
,则这两个向量的位置关系是___________。