题目内容
四棱锥P—ABCD中,底面ABCD是矩形,△PCD为正三角形,平面PCD⊥平面ABCD,PB⊥AC,E为PD中点.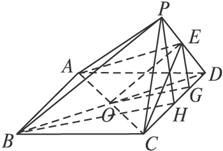
(1)求证:PB∥平面AEC;
(2)求二面角E-A-C-D的大小.
解:(1)证明:连BD交AC于点O,连结OE,

∵E为PD中点,O为BD中点,
∴OE∥PB.
∵OE![]() 平面AEC,PB
平面AEC,PB![]() 平面AEC,
平面AEC,
∴PB∥平面AEC.
(2)设CD=a,AD=b,
过P作PH⊥CD,垂足为H,连结BH,
∵平面PCD⊥平面ABCD,∴PH⊥平面ABCD.
∵PB⊥AC,∴BH⊥AC.
取HD中点G,连结EG、OG,则EG![]()
![]() PH,OG
PH,OG![]()
![]() BH,
BH,
∴OG⊥AC.
∵PB∥EO,PB⊥AC,∴EO⊥AC.
∴∠EOG为二面角EACD的平面角.
∵BH⊥AC,∴∠BHC=∠ACB.
∴![]() .∴
.∴![]() ,a=
,a=![]() b.
b.
EG=![]() PH=
PH=![]() b,EO=
b,EO=![]() b,
b,
∴sin∠EOG=![]() ∴∠EOG=
∴∠EOG=![]() .
.
∴二面角E-AC-D的大小为![]() .
.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
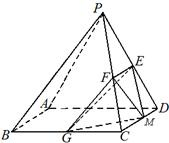 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.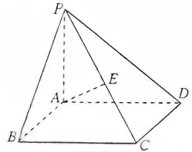 (2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2
(2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2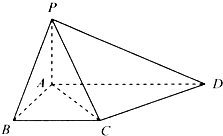 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC= 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点. 如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.