Question

【题目】如图，已知椭圆 （a＞b＞0）的左右顶点分别是A（﹣ ，0），B（ ，0），离心率为 ．设点P（a，t）（t≠0），连接PA交椭圆于点C，坐标原点是O．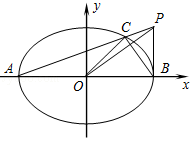

（Ⅰ）证明：OP⊥BC；
（Ⅱ）若三角形ABC的面积不大于四边形OBPC的面积，求|t|的最小值．

Answer 1

【答案】解：（Ⅰ）由题意可知：a= ，e= = = ，则b=1，
∴椭圆的标准方程： ，
设直线PA的方程y= （x+ ），
则 ，
整理得：（4+t2）x2+2 t2x+2t2﹣8=0，
解得：x1=﹣ ，x2= ，则C点坐标（ ， ），
故直线BC的斜率kBC=﹣ ，直线OP的斜率kOP= ，
∴kBCkOP=﹣1，
∴OP⊥BC；
（Ⅱ）由（Ⅰ）可知：四边形OBPC的面积S1= ×丨OP丨×丨BC丨= ，
则三角形ABC，S2= ×2 × = ，
由 ≤ ，整理得：t2+2≥4，则丨t丨≥ ，
∴丨t丨min= ，
|t|的最小值 ．
【解析】（Ⅰ）由a= ，椭圆的离心率e= = ，求得b，求得椭圆的标准方程，求得直线PA的方程，求得C点坐标，直线BC的斜率kBC=﹣ ，直线OP的斜率kBC= ，则kBCkBC=﹣1，则OP⊥BC；（Ⅱ）分别求得三角形ABC的面积和四边形OBPC的面积，由题意即可求得|t|的最小值．