题目内容
已知定义域是全体实数的函数y=f(x)满足f(x+2π)=f(x),且函数g(x)=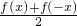 ,函数h(x)=
,函数h(x)=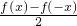 .现定义函数p(x),q(x)为:p(x)=
.现定义函数p(x),q(x)为:p(x)=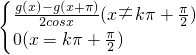 ,q(x)=
,q(x)=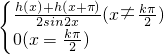 ,其中k∈Z,那么下列关于p(x),q(x)叙述正确的是
,其中k∈Z,那么下列关于p(x),q(x)叙述正确的是
- A.都是奇函数且周期为π
- B.都是偶函数且周期为π
- C.均无奇偶性但都有周期性
- D.均无周期性但都有奇偶性
B
分析:先求出g(-x)= =g(x),再利用f(x)的周期为2π,可推出g(x+π)=g(x-π),故g(x)周期为
=g(x),再利用f(x)的周期为2π,可推出g(x+π)=g(x-π),故g(x)周期为
2π,在此基础上推出p(-x)=p(x),p(x+π)=p(x),即p(x)是偶函数且周期为π,同理可得q(x)
也是偶函数且周期为π.
解答:∵g(x)=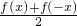 ,∴g(-x)=
,∴g(-x)= =g(x) 且g(x+π)=
=g(x) 且g(x+π)= =g(x-π),即g(x)周期为2π.
=g(x-π),即g(x)周期为2π.
∴x≠kπ+ 时,p(-x)=
时,p(-x)= =
= ,
,
且p(x+π)= ,由此可得p(x)是偶函数且周期为π,
,由此可得p(x)是偶函数且周期为π,
同理可得q(x)也是偶函数且周期为π.
故选B.
点评:本题考查了抽象函数的奇偶性及其周期性,此类考点具有很强的抽象性,因而难度较大.
分析:先求出g(-x)=
 =g(x),再利用f(x)的周期为2π,可推出g(x+π)=g(x-π),故g(x)周期为
=g(x),再利用f(x)的周期为2π,可推出g(x+π)=g(x-π),故g(x)周期为2π,在此基础上推出p(-x)=p(x),p(x+π)=p(x),即p(x)是偶函数且周期为π,同理可得q(x)
也是偶函数且周期为π.
解答:∵g(x)=
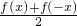 ,∴g(-x)=
,∴g(-x)= =g(x) 且g(x+π)=
=g(x) 且g(x+π)= =g(x-π),即g(x)周期为2π.
=g(x-π),即g(x)周期为2π.∴x≠kπ+
 时,p(-x)=
时,p(-x)= =
= ,
,且p(x+π)=
 ,由此可得p(x)是偶函数且周期为π,
,由此可得p(x)是偶函数且周期为π,同理可得q(x)也是偶函数且周期为π.
故选B.
点评:本题考查了抽象函数的奇偶性及其周期性,此类考点具有很强的抽象性,因而难度较大.

练习册系列答案
相关题目
 ,函数h(x)=
,函数h(x)= .现定义函数p(x),q(x)为:p(x)=
.现定义函数p(x),q(x)为:p(x)= ,q(x)=
,q(x)= ,其中k∈Z,那么下列关于p(x),q(x)叙述正确的是( )
,其中k∈Z,那么下列关于p(x),q(x)叙述正确的是( )