题目内容
实数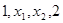 成等差数列,
成等差数列,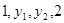 成等比数列,则
成等比数列,则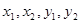 的大小关系是( )
的大小关系是( )
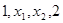 成等差数列,
成等差数列,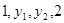 成等比数列,则
成等比数列,则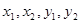 的大小关系是( )
的大小关系是( )A.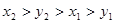 | B. |
C.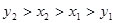 | D.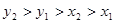 |
A
试题分析:根据等差数列的性质,由于实数
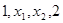 成等差数列,故有
成等差数列,故有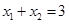 ,且等差数列的通项公式可知公差为d=
,且等差数列的通项公式可知公差为d=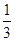 ,
,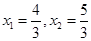 ,
,又
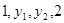 成等比数列,结合等比中项的性质可知,
成等比数列,结合等比中项的性质可知,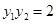 ,那么可知公比为
,那么可知公比为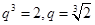 ,那么
,那么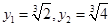 ,通过平方作差可以比较大小得到为选项A.
,通过平方作差可以比较大小得到为选项A.点评:解决该试题的关键是能利用已知中的数列的项求解出各个项的值,然后结合指数幂的运算来比较大小得到结论,属于基础题。

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
 中,
中,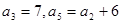 ,则
,则 .
.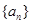 是递增的等差数列,
是递增的等差数列,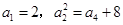 .
.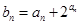 ,求数列
,求数列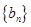 的前
的前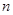 项和
项和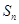 .
. 的各项排成如图所示的三角形数阵,数阵中每一行的第一个数
的各项排成如图所示的三角形数阵,数阵中每一行的第一个数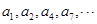 构成等差数列
构成等差数列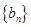 ,
,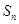 是
是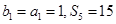
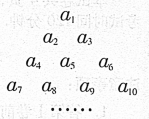
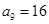 ,求
,求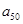 的值;
的值;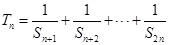 ,求
,求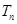 .
. 和
和 满足
满足 ,
, ,
, 。
。 为等差数列,并求数列
为等差数列,并求数列 项和为
项和为 ,令
,令 ,求
,求 的最小值。
的最小值。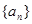 的前n项和为
的前n项和为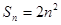
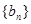 为等比数列,且
为等比数列,且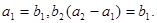
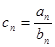 ,求数列
,求数列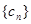 的前n项和
的前n项和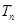 。
。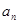 }中,al=1,a2=2,2
}中,al=1,a2=2,2 2+
2+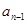 2 (n≥2),则a6等于
2 (n≥2),则a6等于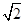
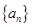 的前
的前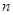 项和为
项和为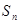 .已知
.已知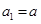 ,
,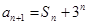 ,
, .
.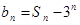 ,求数列
,求数列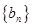 的通项公式;
的通项公式;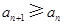 ,
,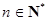 ,求
,求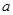 的取值范围.
的取值范围. 的正整数表示成各项都是整数,公差为2的等差数列前
的正整数表示成各项都是整数,公差为2的等差数列前 项的和,称作“对
项的和,称作“对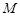 的
的 项分划”,例如:
项分划”,例如: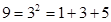 ,称作“对9的3项分划”;
,称作“对9的3项分划”;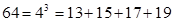 称作“对64的4项分划”,据此对324的18项分划中最大的数是
称作“对64的4项分划”,据此对324的18项分划中最大的数是