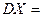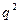题目内容
(本小题满分12分)甲有一个装有 个红球、
个红球、 个黑球的箱子,乙有一个装有
个黑球的箱子,乙有一个装有 个红球、
个红球、 个黑球的箱子,两人各自从自己的箱子里任取一球,并约定:所取两球同色时甲胜,异色时乙胜(
个黑球的箱子,两人各自从自己的箱子里任取一球,并约定:所取两球同色时甲胜,异色时乙胜( ,
, ,
, ,
,
 ).
).
(Ⅰ)当 ,时,求甲获胜的概率;
,时,求甲获胜的概率;
(Ⅱ)当 ,
, 时,规定:甲取红球获胜得3分;取黑球获胜得1分;甲负得0分.求甲的得分期望达到最大时的
时,规定:甲取红球获胜得3分;取黑球获胜得1分;甲负得0分.求甲的得分期望达到最大时的 ,
, 值;
值;
(Ⅲ)当 时,这个游戏规则公平吗?请说明理由.
时,这个游戏规则公平吗?请说明理由.
 个红球、
个红球、 个黑球的箱子,乙有一个装有
个黑球的箱子,乙有一个装有 个红球、
个红球、 个黑球的箱子,两人各自从自己的箱子里任取一球,并约定:所取两球同色时甲胜,异色时乙胜(
个黑球的箱子,两人各自从自己的箱子里任取一球,并约定:所取两球同色时甲胜,异色时乙胜( ,
, ,
, ,
,
 ).
).(Ⅰ)当
 ,时,求甲获胜的概率;
,时,求甲获胜的概率;(Ⅱ)当
 ,
, 时,规定:甲取红球获胜得3分;取黑球获胜得1分;甲负得0分.求甲的得分期望达到最大时的
时,规定:甲取红球获胜得3分;取黑球获胜得1分;甲负得0分.求甲的得分期望达到最大时的 ,
, 值;
值;(Ⅲ)当
 时,这个游戏规则公平吗?请说明理由.
时,这个游戏规则公平吗?请说明理由.解:(Ⅰ)由题意,甲、乙都取红球的概率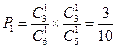 ,
,
甲、乙都取黑球的概率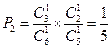 ,∴甲获胜的概
,∴甲获胜的概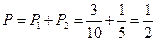 .……… 3分
.……… 3分
(Ⅱ)令 表示甲的分数,则
表示甲的分数,则 的取值为0,1,3,
的取值为0,1,3,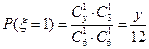 ,
,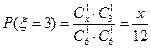 ,
, 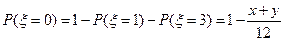 ,
,
得 的分布列如下:
的分布列如下:
于是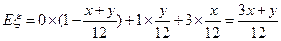 ;
;
又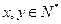 且
且 ,∴
,∴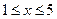 ,且
,且 
故当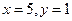 时,
时,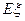 的最大值为
的最大值为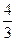 . ……………………………… 7分
. ……………………………… 7分
(Ⅲ)由题意,两人各自从自己的箱子里任取一球比颜色共有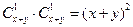 种不同情形,
种不同情形,
每种情形都是等可能的,记甲获胜为事件A,乙获胜为事件B,则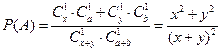 ,
,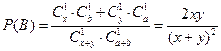 ,
,
∴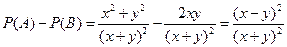 ,
,
当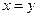 时,
时,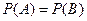 ,甲、乙获胜的概率相等,这个游戏规则是公平的;
,甲、乙获胜的概率相等,这个游戏规则是公平的;
当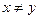 时,
时,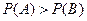 ,甲获胜的概率大于乙获胜的概率,这个游戏规则不公平,有利于甲.
,甲获胜的概率大于乙获胜的概率,这个游戏规则不公平,有利于甲.
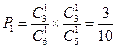 ,
, 甲、乙都取黑球的概率
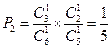 ,∴甲获胜的概
,∴甲获胜的概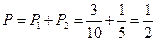 .……… 3分
.……… 3分(Ⅱ)令
 表示甲的分数,则
表示甲的分数,则 的取值为0,1,3,
的取值为0,1,3,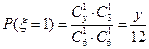 ,
,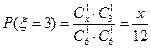 ,
, 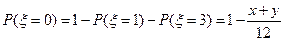 ,
,  | 0 | 1 | 3 |
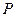 |  | 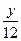 | 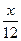 |
 的分布列如下:
的分布列如下:于是
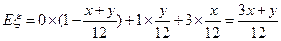 ;
; 又
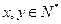 且
且 ,∴
,∴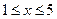 ,且
,且 
故当
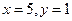 时,
时,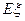 的最大值为
的最大值为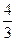 . ……………………………… 7分
. ……………………………… 7分(Ⅲ)由题意,两人各自从自己的箱子里任取一球比颜色共有
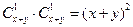 种不同情形,
种不同情形,每种情形都是等可能的,记甲获胜为事件A,乙获胜为事件B,则
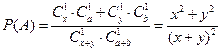 ,
,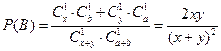 ,
,∴
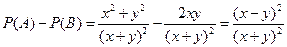 ,
, 当
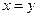 时,
时,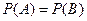 ,甲、乙获胜的概率相等,这个游戏规则是公平的;
,甲、乙获胜的概率相等,这个游戏规则是公平的;当
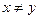 时,
时,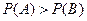 ,甲获胜的概率大于乙获胜的概率,这个游戏规则不公平,有利于甲.
,甲获胜的概率大于乙获胜的概率,这个游戏规则不公平,有利于甲.略

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
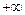 )
) ,则
,则 等于( )
等于( )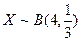 ,则
,则