题目内容
袋中装有大小相同标号不同的白球4个,黑球5个,从中任取3个球.
(1)共有多少种不同结果?
(2)取出的3球中有2个白球,1个黑球的结果有几个?
(3)取出的3球中至少有2个白球的结果有几个?
(4)计算第(2)、(3)小题表示的事件的概率
(1)共有多少种不同结果?
(2)取出的3球中有2个白球,1个黑球的结果有几个?
(3)取出的3球中至少有2个白球的结果有几个?
(4)计算第(2)、(3)小题表示的事件的概率
(1)设从4个白球,5个黑球中任取3个的所有结果组成的集合为I.
∴card(I)=C.
∴共有C=84个不同结果.
(2)设事件:“取出3球中有2个白球,1个黑球”的所有结果组成的集合为A.
∴card(A)=CC.
∴共有CC=30种不同的结果.
(3)设事件:“取出3球中至少有2个白球”的所有结果组成集合为B.
∴card(B)=C+CC.
∴共有C+CC=34种不同的结果.
(4)∵从4个白球,5个黑球中,任取3个球的所有结果的出现可能性都相同,
∴第(2)小题的事件发生的概率为=,
第(3)小题的事件发生的概率为=.
∴card(I)=C.
∴共有C=84个不同结果.
(2)设事件:“取出3球中有2个白球,1个黑球”的所有结果组成的集合为A.
∴card(A)=CC.
∴共有CC=30种不同的结果.
(3)设事件:“取出3球中至少有2个白球”的所有结果组成集合为B.
∴card(B)=C+CC.
∴共有C+CC=34种不同的结果.
(4)∵从4个白球,5个黑球中,任取3个球的所有结果的出现可能性都相同,
∴第(2)小题的事件发生的概率为=,
第(3)小题的事件发生的概率为=.
略

练习册系列答案
相关题目
 个红球、
个红球、 个黑球的箱子,乙有一个装有
个黑球的箱子,乙有一个装有 个红球、
个红球、 个黑球的箱子,两人各自从自己的箱子里任取一球,并约定:所取两球同色时甲胜,异色时乙胜(
个黑球的箱子,两人各自从自己的箱子里任取一球,并约定:所取两球同色时甲胜,异色时乙胜( ).
). ,时,求甲获胜的概率;
,时,求甲获胜的概率; ,
, 时,规定:甲取红球获胜得3分;取黑球获胜得1分;甲负得0分.求甲的得分期望达到最大时的
时,规定:甲取红球获胜得3分;取黑球获胜得1分;甲负得0分.求甲的得分期望达到最大时的 时,这个游戏规则公平吗?请说明理由.
时,这个游戏规则公平吗?请说明理由. ,若中奖,则家具城返还顾客现金200元. 某顾客购买一张价格为3400元的餐桌,得到3张奖券.
,若中奖,则家具城返还顾客现金200元. 某顾客购买一张价格为3400元的餐桌,得到3张奖券.
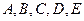 的5张卡片排成一排,在第一张是
的5张卡片排成一排,在第一张是 且第三张是
且第三张是 的条件下,第二张是
的条件下,第二张是 的概率为 ;第二张是
的概率为 ;第二张是 B.
B.  C.
C. 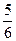 D.
D. 