题目内容
给出下列四个函数:①y=sinx+cosx;②y=sinx-cosx;③y=sinx•cosx;④
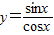 .其中在
.其中在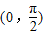 上既无最大值又无最小值的函数是 .(写出全部正确结论的序号)
上既无最大值又无最小值的函数是 .(写出全部正确结论的序号)
【答案】分析:①②③都可以化为y=Asin(ωx+φ)形式,结合正弦函数的图象求最值,
④可从几何意义入手,看作单位圆上的点与原点连线的斜率,从而求范围.
解答:解:①y=sinx+cosx=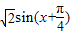 ,
,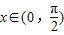 ,
,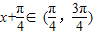 ,y
,y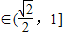 ,有最大值1;
,有最大值1;
②y=sinx-cosx=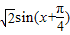 ,
,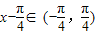 ,y
,y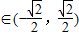 ,无最大和最小值;
,无最大和最小值;
③y=sinx•cosx= sin2x∈
sin2x∈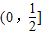 ,有最大值;
,有最大值;
④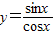 表示单位圆上的点与原点连线的斜率的范围,属于R,无最大和最小值.
表示单位圆上的点与原点连线的斜率的范围,属于R,无最大和最小值.
故答案为:②④
点评:本题考查三角函数的值域问题,注意数形结合思想的应用.
④可从几何意义入手,看作单位圆上的点与原点连线的斜率,从而求范围.
解答:解:①y=sinx+cosx=
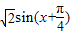 ,
,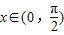 ,
,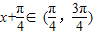 ,y
,y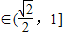 ,有最大值1;
,有最大值1;②y=sinx-cosx=
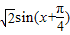 ,
,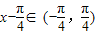 ,y
,y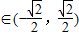 ,无最大和最小值;
,无最大和最小值;③y=sinx•cosx=
 sin2x∈
sin2x∈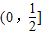 ,有最大值;
,有最大值;④
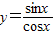 表示单位圆上的点与原点连线的斜率的范围,属于R,无最大和最小值.
表示单位圆上的点与原点连线的斜率的范围,属于R,无最大和最小值.故答案为:②④
点评:本题考查三角函数的值域问题,注意数形结合思想的应用.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目