题目内容
设函数f （x）的定义域为D，如果对于任意的x1∈D，存在唯一的x2∈D，使| f(x1)+f(x2) | 2 |
则满足在其定义域上均值为2的函数是
分析：首先分析题目求对于任意的x1∈D，存在唯一的x2∈D，使
=2成立的函数．
对于函数①y=x3，可直接取任意的x1∈R，验证求出唯一的x2=
，即可得到成立．
对于函数②y=4sinx，因为y=4sinx是R上的周期函数，明显不成立．
对于函数③y=lgx，定义域为x＞0，值域为R且单调，显然成立．
对于函数④y=2x，特殊值法代入验证不成立成立．即可得到答案．
| f(x1)+f(x2) |
| 2 |
对于函数①y=x3，可直接取任意的x1∈R，验证求出唯一的x2=
| 3 | 4-
| ||
对于函数②y=4sinx，因为y=4sinx是R上的周期函数，明显不成立．
对于函数③y=lgx，定义域为x＞0，值域为R且单调，显然成立．
对于函数④y=2x，特殊值法代入验证不成立成立．即可得到答案．
解答：解：对于函数①y=x3，取任意的x1∈R，
=
=2，x2=
，可以得到唯一的x2∈D．故满足条件．
对于函数②y=4sinx，明显不成立，因为y=4sinx是R上的周期函数，存在无穷个的x2∈D，使
=2成立．故不满足条件．
对于函数③y=lgx，定义域为x＞0，值域为R且单调，显然必存在唯一的x2∈D，使
=2成立．故成立．
对于函数④y=2x定义域为R，值域为y＞0．对于x1=3，f（x1）=8．要使
=2成立，则f（x2）=-4，不成立．
故答案为①③．
| f(x1)+f(x2) |
| 2 |
| ||||
| 2 |
| 3 | 4-
| ||
对于函数②y=4sinx，明显不成立，因为y=4sinx是R上的周期函数，存在无穷个的x2∈D，使
| f(x1)+f(x2) |
| 2 |
对于函数③y=lgx，定义域为x＞0，值域为R且单调，显然必存在唯一的x2∈D，使
| f(x1)+f(x2) |
| 2 |
对于函数④y=2x定义域为R，值域为y＞0．对于x1=3，f（x1）=8．要使
| f(x1)+f(x2) |
| 2 |
故答案为①③．
点评：此题主要应用新定义的方式考查平均值不等式在函数中的应用．对于新定义的问题，需要认真分析定义内容，切记不可偏离题目．
练习册系列答案
相关题目
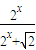的图象上两点P1（x1，y1） P2（x2，y2），若
=
（
+
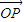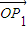），且点P的横坐标为
（1）求证：P点的纵坐标为定值，并求出这个定值；（2）若Sn=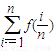
，n∈N*，求Sn；
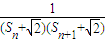}的前n项和，若Tn＜a（
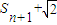）对一切n∈N*都成立，试求a的取值范围
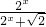的图象上两点P1（x1，y1）、P2（x2，y2），若
=
（
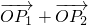），且点P的横坐标为
）+f（
）+A+f（
）+f（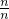
）
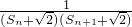}的前n项和，若Tn＜a（Sn+1+
）对一切n∈N*都成立，试求a的取值范围．
．
，③