题目内容
20.某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)在某一个周期内的图象时,列表并填入了部分数据,如表:| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{3}$ | $\frac{5π}{6}$ | |||
| Asin(ωx+φ) | 0 | 5 | -5 | 0 |
(2)将y=f(x)的图象向左平移$\frac{π}{6}$个单位,得到函数y=g(x)的图象.若关于x的方程g(x)-(2m+1)=0在[0,$\frac{π}{2}$]上有两个不同的解,求实数m的取值范围.
分析 (1)根据五点法进行求解即可.
(2)根据函数平移关系求出函数g(x)的表达式,利用函数和方程之间的关系转化为两个函数的交点问题即可.
解答 解:(1)根据表中已知数据,解得A=5,ω=2,φ=-$\frac{π}{6}$,数据补全如下表:
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{12}$ | $\frac{π}{3}$ | $\frac{7π}{12}$ | $\frac{5π}{6}$ | $\frac{13π}{12}$ |
| Asin(ωx+φ) | 0 | 5 | 0 | -5 | 0 |
(2)通过平移,g(x)=5sin(2x+$\frac{π}{6}$),方程g(x)-(2m+1)=0可看成函数g(x),x∈[0,$\frac{π}{2}$]和函数y=2m+1的图象有两个交点,当x∈[0,$\frac{π}{2}$]时,
2x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{7π}{6}$],为使横线y=2m+1与函数g(x)有两个交点,只需$\frac{5}{2}$≤2m+1<5,解得$\frac{3}{4}$≤m<2.
点评 本题主要考查三角函数的图象和性质,利用五点法以及函数与方程的关系进行转化是解决本题的关键.

练习册系列答案
相关题目
15.由点P向圆x2+y2=2引两条切线PA,PB,A,B是切点,则$\overrightarrow{PA}$•$\overrightarrow{PB}$的最小值是( )
| A. | 6-4$\sqrt{2}$ | B. | 3-2$\sqrt{2}$ | C. | 2$\sqrt{2}$-3 | D. | 4$\sqrt{2}$-6 |
5.已知函数f(x)=x2+(a+8)x+a2+a-12,且f(a2-4)=f(2a-8),设等差数列{an}的前n项和为Sn,(n∈N*)若Sn=f(n),则$\frac{{S}_{n}-4a}{{a}_{n}-1}$的最小值为( )
| A. | $\frac{27}{6}$ | B. | $\frac{35}{8}$ | C. | $\frac{14}{3}$ | D. | $\frac{37}{8}$ |
9.若f(x)和g(x)都是定义在R上的奇函数,且F(x)=f(g(x))+2在(0,+∞)上有最大值8,则在(-∞,0)上,F(x)有( )
| A. | 最小值-8 | B. | 最大值-8 | C. | 最小值-6 | D. | 最小值-4 |
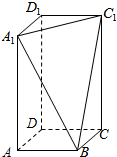 在长方体ABCD-A1B1C1D1中,AB=BC=1,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为$\frac{5}{3}$.则长方体外接球的表面积是6π.
在长方体ABCD-A1B1C1D1中,AB=BC=1,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为$\frac{5}{3}$.则长方体外接球的表面积是6π.
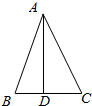 在△ABC中,AD⊥BC,垂足为D,AD在△ABC的内部,且BD:DC:AD=2:3:6,则∠BAC=$\frac{π}{4}$.
在△ABC中,AD⊥BC,垂足为D,AD在△ABC的内部,且BD:DC:AD=2:3:6,则∠BAC=$\frac{π}{4}$.