题目内容
【题目】已知椭圆具有如下性质:若椭圆的方程为![]() ,则椭圆在其上一点
,则椭圆在其上一点![]() 处的切线方程为
处的切线方程为![]() ,试运用该性质解决以下问题:椭圆
,试运用该性质解决以下问题:椭圆![]() :
:![]() ,其焦距为2,且过点
,其焦距为2,且过点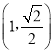 .点
.点![]() 为
为![]() 在第一象限中的任意一点,过
在第一象限中的任意一点,过![]() 作
作![]() 的切线
的切线![]() ,
,![]() 分别与
分别与![]() 轴和
轴和![]() 轴的正半轴交于
轴的正半轴交于![]() 两点,则
两点,则![]() 面积的最小值为( )
面积的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
根据题意,椭圆的焦点为![]() ,
,![]() ,可得
,可得![]() ,代入点
,代入点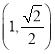 ,计算即可求出
,计算即可求出![]() ,从而可求椭圆
,从而可求椭圆![]() 的方程;设
的方程;设![]() ,求得椭圆
,求得椭圆![]() 在点
在点![]() 处的切线方程,分别令
处的切线方程,分别令![]() ,求得截距,由三角形的面积公式,再结合基本不等式,即可求
,求得截距,由三角形的面积公式,再结合基本不等式,即可求![]() 面积的最小值.
面积的最小值.
由题意可得![]() ,即
,即![]() ,代入点
,代入点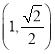 ,可得
,可得![]() ,
,
解得![]() ,即有椭圆的方程为
,即有椭圆的方程为![]() ,
,
设![]() ,则椭圆
,则椭圆![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]()
令![]() ,令
,令![]() ,可得
,可得![]() ,
,
所以![]() ,又点
,又点![]() 在椭圆的第一象限上,
在椭圆的第一象限上,
所以![]() ,即有
,即有
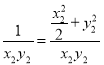
![]()
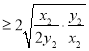
![]()
![]() ,当且仅当
,当且仅当![]() ,
,
所以当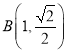 时,则
时,则![]() 的面积的最小值为
的面积的最小值为![]() .
.
故选:![]()

练习册系列答案
相关题目
【题目】为降低汽车尾气的排放量,某厂生产甲乙两种不同型号的节排器,分别从甲乙两种节排器中各自抽取100件进行性能质量评估检测,综合得分情况的频率分布直方图如图所示.
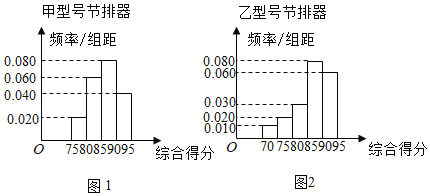
节排器等级及利润如表格表示,其中![]()
综合得分 | 节排器等级 | 节排器利润率 |
| 一级品 |
|
| 二级品 |
|
| 三级品 |
|
(1)若从这100件甲型号节排器按节排器等级分层抽样的方法抽取10件,再从这10件节排器中随机抽取3件,求至少有2件一级品的概率;
(2)视频率分布直方图中的频率为概率,用样本估计总体,则
①若从乙型号节排器中随机抽取3件,求二级品数![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
②从长期来看,骰子哪种型号的节排器平均利润较大?