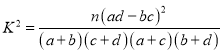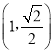题目内容
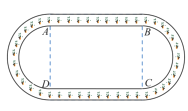
【题目】某公司设计如图所示的环状绿化景观带,该景观带的内圈由两条平行线段(图中的![]() )和两个半圆构成,设
)和两个半圆构成,设![]() ,且
,且![]() .
.
(1)若内圈周长为![]() ,则
,则![]() 取何值时,矩形
取何值时,矩形![]() 的面积最大?
的面积最大?
(2)若景观带的内圈所围成区域的面积为![]() ,则
,则![]() 取何值时,内圈周长最小?
取何值时,内圈周长最小?
【答案】(1)100(2)340
【解析】
试题(1)依据题设条件建立目标函数![]() ,然后运用基本不等式确定其取最大值时
,然后运用基本不等式确定其取最大值时![]() 的取值;(2)借助题设条件建立内圈周长的目标函数
的取值;(2)借助题设条件建立内圈周长的目标函数![]() ,然后运用导数知识求其取得最小值时
,然后运用导数知识求其取得最小值时![]() 的取值:
的取值:
解:设题中半圆形半径为![]() ,矩形
,矩形![]() 的面积为
的面积为![]() ,
,
内圈周长为![]() .
.
(1)由题意知:![]() ,且
,且![]() ,即
,即![]() ,
,
于是![]()
当且仅当![]() 时,等号成立.
时,等号成立.
答:当![]() 时,矩形
时,矩形![]() 的面积最大.
的面积最大.

(2)由题意知:![]() ,于是
,于是![]() ,
,
从而![]() .
.
因为![]() ,所以
,所以![]() ,即
,即![]() ,
,
解得![]() ,所以
,所以![]() ,故
,故![]() .
.
因为![]() ,
,
所以关于![]() 的函数
的函数![]() 在
在![]() 上是单调减函数.
上是单调减函数.
故当![]() 即
即![]() 时,内圈周长
时,内圈周长![]() 取得最小值,
取得最小值,
且最小值为![]() .
.

练习册系列答案
相关题目
【题目】微信是现代生活中进行信息交流的重要工具.据统计,某公司200名员工中![]() 的人使用微信,其中每天使用微信时间少于一小时的有60人,其余的员工每天使用微信时间不少于一小时,若将员工分成青年(年龄小于40岁)和中年(年龄不小于40岁)两个阶段,那么使用微信的人中
的人使用微信,其中每天使用微信时间少于一小时的有60人,其余的员工每天使用微信时间不少于一小时,若将员工分成青年(年龄小于40岁)和中年(年龄不小于40岁)两个阶段,那么使用微信的人中![]() 是青年人.若规定:每天使用微信时间不少于一小时为经常使用微信,那么经常使用微信的员工中
是青年人.若规定:每天使用微信时间不少于一小时为经常使用微信,那么经常使用微信的员工中![]() 都是青年人.
都是青年人.
(1)若要调查该公司使用微信的员工经常使用微信与年龄的关系,完成![]() 列联表:
列联表:
青年人 | 中年人 | 合计 | |
经常使用微信 | |||
不经常使用微信 | |||
合计 |
(2)由列联表中所得数据判断,能否在犯错误的概率不超过![]() 的前提下认为“经常使用微信与年龄有关”?
的前提下认为“经常使用微信与年龄有关”?
| 0.010 | 0.001 |
| 6.635 | 10.828 |
![]()