题目内容
10.设fn(x)=(1+x)n,n∈N*(1)若g(x)=f6(x)+2f7(x)+3f8(x),求g(x)中含x6项的系数;
(2)若h(x)=fn(x)+fn($\frac{1}{x}$),求h2011(x)在区间[$\frac{1}{3}$,2]上的最大值与最小值;
(3)证明:Cmm+2Cmm+1+3Cmm+2+…+nCmm+n-1=$\frac{(m+1)n+1}{m+2}$•Cm+1m+n(m,n∈N*)
分析 (1)由条件求得g(x)的解析式,可得g(x)中含x6项的系数.
(2)化简h2011(x)可得它在(0,1)上递减,(1,+∞)递增,由此求得它在区间[$\frac{1}{3}$,2]上的最值.
(3)设m(x)=(1+x)m+2•(1+x)m+1+3•(1+x)m+2+…+n•(1+x)m+n-1…①,则(1+x)m(x)=(1+x)m+1+2•(1+x)m+2+…+n•(1+x)m+n…②,两式相减求得 x2•m(x)=(1+x)m-(1+x)m+n+nx•(1+x)m+n,故m(x)中含xm项的系数即 x2•m(x)中含xm+2项的系数.再利用组合数的计算公式证得结论成立.
解答 解:(1)∵fn(x)=(1+x)n,n∈N*,故g(x)=f6(x)+2f7(x)+3f8(x)
=(1+x)6 +2(1+x)7+3(1+x)8 ,
故g(x)中含x6项的系数为${C}_{6}^{6}$+2${C}_{7}^{6}$+3${C}_{8}^{6}$=99.
(2)h2011(x)=(1+x)2011 +${(1+\frac{1}{x})}^{2011}$=(${C}_{2011}^{0}$+${C}_{2011}^{0}$)+(${C}_{2011}^{1}$•x+${C}_{2011}^{1}$•$\frac{1}{x}$)
+(${C}_{2011}^{2}$•x2+${C}_{2011}^{2}$•$\frac{1}{{x}^{2}}$)+…+(${C}_{2011}^{2011}$•x2011+${C}_{2011}^{2011}$•$\frac{1}{{x}^{2011}}$),
展开式中所有${{C}_{2011}^{k}{x}^{k}}^{\;}$+${C}_{2011}^{k}(\frac{1}{x})^{k}$组合都是(0,1)上递减,(1,+∞)递增,
在区间[$\frac{1}{3}$,2]上,
故当x=1时,h2011(x)取得最小值为h2011(1)=2•22011=24022,当x=$\frac{1}{3}$时,h2011(x)取得最大值
为h2011($\frac{1}{3}$)=${(\frac{4}{3})}^{2011}$+42011.
(3)证明:设m(x)=(1+x)m+2•(1+x)m+1+3•(1+x)m+2+…+n•(1+x)m+n-1…①,
则m(x)中含xm 项的系数为${C}_{m}^{m}$+2${C}_{m+1}^{m}$+3•${C}_{m+2}^{m}$+…+n${C}_{m+n-1}^{m}$.
(1+x)m(x)=(1+x)m+1+2•(1+x)m+2+…+n•(1+x)m+n…②,
①-②可得-xm(x)=(1+x)m+(1+x)m+1+(1+x)m+2+…+(1+x)m+n-1-n•(1+x)m+n,
=$\frac{{(1+x)}^{m}•[1{-(1+x)}^{n}]}{1-(1+x)}$-n•(1+x)m+n,
∴x2•m(x)=(1+x)m-(1+x)m+n+nx•(1+x)m+n,
故m(x)中含xm项的系数即 x2•m(x)中含xm+2项的系数,
而x2•m(x)中含xm+2项的系数为-${C}_{m+n}^{m+2}$+n•${C}_{m+n}^{m+1}$=-$\frac{(m+n)!}{(m+2)!(n-2)!}$+$\frac{n(m+n)!}{(m+1)!(n-1)!}$
=$\frac{-(n-1)+n(m+2)}{m+2}$•$\frac{(m+n)!}{(m+1)!(n-1)!}$=$\frac{(m+1)n+1}{m+2}$•${C}_{m+n}^{m+1}$,
∴Cmm+2Cmm+1+3Cmm+2+…+nCmm+n-1=$\frac{(m+1)n+1}{m+2}$•Cm+1m+n(m,n∈N*).
点评 本题主要考查二项式定理的应用,二项展开式的同项公式,组合数的计算公式的应用,属于难题.

| A. | g(x1)<0,f(x2)>0 | B. | g(x1)>0,f(x2)<0 | C. | g(x1)>0,f(x2)>0 | D. | g(x1)<0,f(x2)<0 |
| A. | 2$\sqrt{2}$-1 | B. | 2$\sqrt{2}$+1 | C. | 2$\sqrt{2}$-2 | D. | 2$\sqrt{2}$-$\sqrt{5}$ |
| A. | (a,d)∪(b,c) | B. | (c,a]∪[b,d) | C. | (a,c]∪[d,b) | D. | (c,a)∪(d,b) |
| A. | m=-1 | B. | m=-2 | C. | m=-1或2 | D. | m=l或m=-2 |
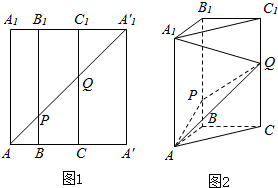 如图1所示,在边长为12的正方形AA′A′1A1中,BB1∥CC1∥AA1,且AB=3,BC=4,AA1′分别交BB1,CC1于点P,Q,将该正方形沿BB1、CC1折叠,使得A′A1′与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1中
如图1所示,在边长为12的正方形AA′A′1A1中,BB1∥CC1∥AA1,且AB=3,BC=4,AA1′分别交BB1,CC1于点P,Q,将该正方形沿BB1、CC1折叠,使得A′A1′与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1中