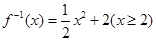题目内容
已知函数f (x)=ax+2-1(a>0,且a≠1)的反函数为 .
.
(1)求 ;(注意:指数为x+2)
;(注意:指数为x+2)
(2)若 在[0,1]上的最大值比最小值大2,求a的值;
在[0,1]上的最大值比最小值大2,求a的值;
(3)设函数 ,求不等式g(x)≤
,求不等式g(x)≤ 对任意的
对任意的 恒成立的x的取值范围.
恒成立的x的取值范围.
 .
.(1)求
 ;(注意:指数为x+2)
;(注意:指数为x+2)(2)若
 在[0,1]上的最大值比最小值大2,求a的值;
在[0,1]上的最大值比最小值大2,求a的值;(3)设函数
 ,求不等式g(x)≤
,求不等式g(x)≤ 对任意的
对任意的 恒成立的x的取值范围.
恒成立的x的取值范围.(1) =loga(x+1)-2(x>-1).(2)
=loga(x+1)-2(x>-1).(2)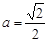 或
或 .
.
(3)满足条件的x的取值范围为 .
.
 =loga(x+1)-2(x>-1).(2)
=loga(x+1)-2(x>-1).(2)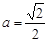 或
或 .
.(3)满足条件的x的取值范围为
 .
.本题考查反函数,考查函数的最值及其几何意义,考查函数恒成立问题,综合性强,考查化归思想、方程思想、分类讨论思想的综合运用,属于难题
(1)由y="f" (x)=ax+2-1,求得x=loga(y+1)-2,即可得f-1(x);
(2)对底数a分a>1与0<a<1两类讨论,分别求得其最大值与最小值,利用f-1(x)在[0,1]上的最大值比最小值大2,即可求得a的值;
(3)由题意可得 转化为不等式x2≤a3+1对任意的 恒成立,从而可求得x的取值范围。
恒成立,从而可求得x的取值范围。
(1)由y="f" (x)=ax+2-1,求得x=loga(y+1)-2,即可得f-1(x);
(2)对底数a分a>1与0<a<1两类讨论,分别求得其最大值与最小值,利用f-1(x)在[0,1]上的最大值比最小值大2,即可求得a的值;
(3)由题意可得 转化为不等式x2≤a3+1对任意的
 恒成立,从而可求得x的取值范围。
恒成立,从而可求得x的取值范围。
练习册系列答案
相关题目
 的反函数
的反函数 ________________.
________________. 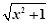 (x≤-1),则f-1(2)= .
(x≤-1),则f-1(2)= . 的图象经过(0,-1),则y=
的图象经过(0,-1),则y= 的反函数图象经过点( )
的反函数图象经过点( )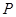 在曲线
在曲线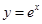 上,点
上,点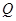 在曲线
在曲线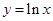 上,则
上,则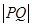 的最小值为( )
的最小值为( )



 ( )
( )

 的图象为
的图象为 ,函数
,函数 的图象为
的图象为 ,若
,若 对称,则
对称,则 .
. 的反函数为( )
的反函数为( )