题目内容
设两个非零向量a与b不共线,
(1)若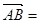 a
a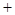 b,
b,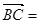 2a
2a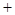 8b,
8b,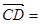 3(a- b)。求证:A、B、D三点共线;
3(a- b)。求证:A、B、D三点共线;
(2)试确定实数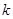 ,使
,使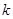 a
a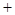 b和a
b和a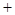
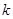 b共线。
b共线。
【答案】
(1)证明三点共线,只要证明任意三点中任取两点得到的两个向量共线即可。
(2)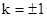
【解析】
试题分析:解(1)证明: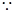
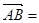 a
a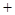 b,
b, 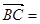 2a
2a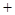 8b,
8b,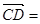 3(a- b)。
3(a- b)。
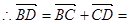 2a
2a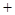 8b
8b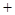 3(a- b)=5(a
3(a- b)=5(a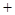 b)=5
b)=5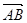 。
。
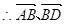 共线,
共线,
又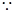 它们有公共点B,所以A、B、D三点共线
它们有公共点B,所以A、B、D三点共线
(2)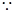
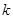 a
a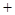 b与a
b与a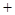
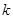 b共线
b共线
所以存在实数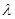 ,使
,使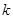 a
a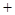 b=
b=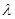 (a
(a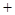
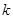 b),
b),
即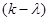 a=
a=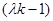 b
b
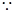 a、b是不共线的两个非零向量,
a、b是不共线的两个非零向量,
所以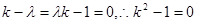
即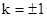
考点:向量共线
点评:主要是考查了向量的共线的运用,属于基础题。

练习册系列答案
相关题目
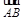 =a+b ,
=a+b ,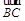 =2a+8b ,
=2a+8b ,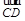 =3(a-b) ,
=3(a-b) ,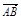 =a+b,
=a+b,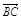 =2a+8b,
=2a+8b,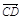 =3(a-b),求证:A、B、D三点共线;
=3(a-b),求证:A、B、D三点共线;