题目内容
【题目】设函数f(x)= ![]() (a>0且a≠1)是定义域为R的奇函数.
(a>0且a≠1)是定义域为R的奇函数.
(1)求t的值;
(2)若f(1)>0,求使不等式f(kx﹣x2)+f(x﹣1)<0对一切x∈R恒成立的实数k的取值范围;
(3)若函数f(x)的图象过点(1, ![]() ),是否存在正数m,且m≠1使函数g(x)=logm[a2x+a﹣2x﹣mf(x)]在[1,log23]上的最大值为0,若存在,求出m的值,若不存在,请说明理由.
),是否存在正数m,且m≠1使函数g(x)=logm[a2x+a﹣2x﹣mf(x)]在[1,log23]上的最大值为0,若存在,求出m的值,若不存在,请说明理由.
【答案】
(1)解:f(x)是定义域为R的奇函数
∴f(0)=0,
∴t=2
(2)解:由(1)得f(x)=ax﹣a﹣x,
∵f(1)>0得 ![]() 又a>0
又a>0
∴a>1,
由f(kx﹣x2)+f(x﹣1)<0得f(kx﹣x2)<﹣f(x﹣1),
∵f(x)为奇函数,
∴f(kx﹣x2)<f(1﹣x),
∵a>1∴f(x)=ax﹣a﹣x为R上的增函数,
∴kx﹣x2<1﹣x对一切x∈R恒成立,即x2﹣(k+1)x+1>0对一切x∈R恒成立
故△=(k+1)2﹣4<0解得﹣3<k<1
(3)解:函数f(x)的图象过点(1, ![]() ),
),
∴a=2,假设存在正数m,且m≠1符合题意,由a=2得 ![]() =
= ![]() =
= ![]()
设t=2x﹣2﹣x则(2x﹣2﹣x)2﹣m(2x﹣2﹣x)+2=t2﹣mt+2,
∵x∈[1,log23],
∴ ![]() 记h(t)=t2﹣mt+2,
记h(t)=t2﹣mt+2,
∵函数 ![]() 在[1,log23]上的最大值为0,
在[1,log23]上的最大值为0,
∴(ⅰ)若0<m<1时,则函数h(t)=t2﹣mt+2在 ![]() 有最小值为1
有最小值为1
由于对称轴 ![]() ∴
∴ ![]() ,不合题意
,不合题意
(ⅱ)若m>1时,则函数h(t)=t2﹣mt+2>0在 ![]() 上恒成立,且最大值为1,最小值大于0
上恒成立,且最大值为1,最小值大于0
① 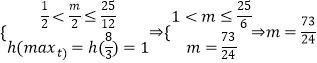
又此时 ![]() ,
, ![]()
故g(x)在[1,log23]无意义
所以 ![]()
②  无解,
无解,
综上所述:故不存在正数m,使函数 ![]() 在[1,log23]上的最大值为0
在[1,log23]上的最大值为0
【解析】(1)由奇函数的性质可知f(0)=0,得出t=2;(2)由f(1)>0得 ![]() 又a>0,求出a>1,判断函数的单调性f(x)=ax﹣a﹣x为R上的增函数,不等式整理为x2﹣(k+1)x+1>0对一切x∈R恒成立,利用判别式法求解即可;(3)把点代入求出a=2,假设存在正数m,构造函数设t=2x﹣2﹣x则(2x﹣2﹣x)2﹣m(2x﹣2﹣x)+2=t2﹣mt+2,对底数m进行分类讨论,判断m的值.
又a>0,求出a>1,判断函数的单调性f(x)=ax﹣a﹣x为R上的增函数,不等式整理为x2﹣(k+1)x+1>0对一切x∈R恒成立,利用判别式法求解即可;(3)把点代入求出a=2,假设存在正数m,构造函数设t=2x﹣2﹣x则(2x﹣2﹣x)2﹣m(2x﹣2﹣x)+2=t2﹣mt+2,对底数m进行分类讨论,判断m的值.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案