题目内容
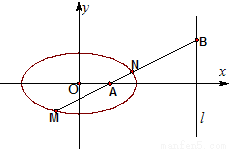
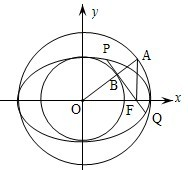
如图,设椭圆C: (a>b>0)的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且
(a>b>0)的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且 ,若过 A,Q,F2三点的圆恰好与直线l:
,若过 A,Q,F2三点的圆恰好与直线l: 相切,过定点 M(0,2)的直线l1与椭圆C交于G,H两点(点G在点M,H之间)。
相切,过定点 M(0,2)的直线l1与椭圆C交于G,H两点(点G在点M,H之间)。
 (a>b>0)的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且
(a>b>0)的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且 ,若过 A,Q,F2三点的圆恰好与直线l:
,若过 A,Q,F2三点的圆恰好与直线l: 相切,过定点 M(0,2)的直线l1与椭圆C交于G,H两点(点G在点M,H之间)。
相切,过定点 M(0,2)的直线l1与椭圆C交于G,H两点(点G在点M,H之间)。
(1)求椭圆C的方程;
(2)设直线l1的斜率k>0,在x轴上是否存在点P(m,0),使得以PG,PH为邻边的平行四边形是菱形?如果存在,求出m的取值范围;如果不存在,请说明理由;
(3)若实数λ满足 ,求λ的取值范围。
,求λ的取值范围。
(2)设直线l1的斜率k>0,在x轴上是否存在点P(m,0),使得以PG,PH为邻边的平行四边形是菱形?如果存在,求出m的取值范围;如果不存在,请说明理由;
(3)若实数λ满足
 ,求λ的取值范围。
,求λ的取值范围。解:(1)因为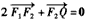
所以F1为F2Q中点
设Q的坐标为(-3c,0),
因为AQ⊥AF2,
所以b2=3c×c=3c2,a2=4c×c=4c2,且过A,Q,F2三点的圆的圆心为F1(-c,0),半径为2c
因为该圆与直线l相切,
所以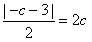
解得c=1,
所以a=2,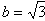
故所求椭圆方程为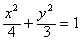 。
。
(2)设l1的方程为y=kx+2(k>0)
由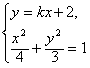 得(3+4k2)x2+16kx+4=0
得(3+4k2)x2+16kx+4=0
设G(x1,y1),H(x2,y2),则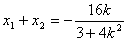
所以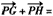 (x1-m,y1)+(x2-m,y2)
(x1-m,y1)+(x2-m,y2)
=(x1+x2-2m,y1+y2)
=(x1+x2-2m,k(x1+x2)+4)
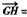 (x2-x1,y2-y1)=(x2-x1,k(x2-x1))
(x2-x1,y2-y1)=(x2-x1,k(x2-x1))
由于菱形对角线互相垂直,因此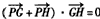
所以(x2-x1)[(x1+x2)-2m]+k(x2-x1)[k(x1+x2)+4]=0
故(x2-x1)[(x1+x2)-2m+k2(x1+x2)+4k]=0
因为k>0,
所以x2-x1≠0
所以(x1+x2)-2m+k2(x1+x2)+4k=0,
即(1+k2)(x1+x2)+4k-2m=0
所以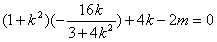
解得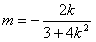
即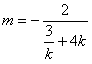
因为k>0,
所以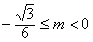
故存在满足题意的点P且m的取值范围是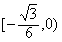 。
。
(3)①当直线l1斜率存在时,
设直线l1方程为y=kx+2,代入椭圆方程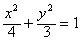
得(3+4k2)x2+16kx+4=0
由△>0,得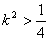
设G(x1,y1),H(x2,y2),
则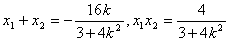
又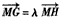 ,
,
所以(x1,y1-2)=λ(x2,y2-2)
所以x1=λx2
所以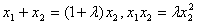
所以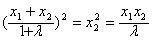
所以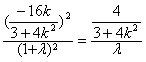
整理得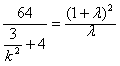
因为,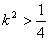
所以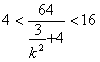 ,即
,即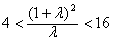
所以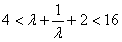
解得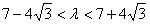
又0<λ<1,
所以7-4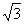 <λ<1。
<λ<1。
②当直线l1斜率不存在时,直线l1的方程为x=0,
此时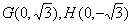 ,
,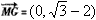 ,
,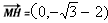 ,
,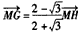
所以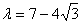
所以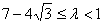 ,
,
即所求λ的取值范围是 。
。
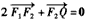
所以F1为F2Q中点
设Q的坐标为(-3c,0),
因为AQ⊥AF2,
所以b2=3c×c=3c2,a2=4c×c=4c2,且过A,Q,F2三点的圆的圆心为F1(-c,0),半径为2c
因为该圆与直线l相切,
所以
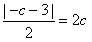
解得c=1,
所以a=2,
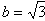
故所求椭圆方程为
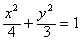 。
。(2)设l1的方程为y=kx+2(k>0)
由
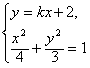 得(3+4k2)x2+16kx+4=0
得(3+4k2)x2+16kx+4=0 设G(x1,y1),H(x2,y2),则
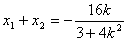
所以
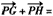 (x1-m,y1)+(x2-m,y2)
(x1-m,y1)+(x2-m,y2) =(x1+x2-2m,y1+y2)
=(x1+x2-2m,k(x1+x2)+4)
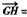 (x2-x1,y2-y1)=(x2-x1,k(x2-x1))
(x2-x1,y2-y1)=(x2-x1,k(x2-x1))由于菱形对角线互相垂直,因此
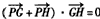
所以(x2-x1)[(x1+x2)-2m]+k(x2-x1)[k(x1+x2)+4]=0
故(x2-x1)[(x1+x2)-2m+k2(x1+x2)+4k]=0
因为k>0,
所以x2-x1≠0
所以(x1+x2)-2m+k2(x1+x2)+4k=0,
即(1+k2)(x1+x2)+4k-2m=0
所以
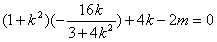
解得
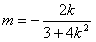
即
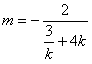
因为k>0,
所以
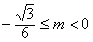
故存在满足题意的点P且m的取值范围是
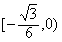 。
。(3)①当直线l1斜率存在时,
设直线l1方程为y=kx+2,代入椭圆方程
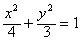
得(3+4k2)x2+16kx+4=0
由△>0,得
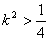
设G(x1,y1),H(x2,y2),
则
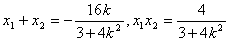
又
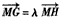 ,
,所以(x1,y1-2)=λ(x2,y2-2)
所以x1=λx2
所以
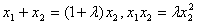
所以
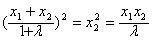
所以
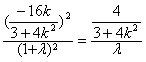
整理得
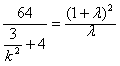
因为,
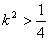
所以
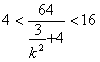 ,即
,即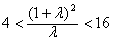
所以
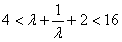
解得
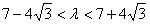
又0<λ<1,
所以7-4
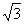 <λ<1。
<λ<1。②当直线l1斜率不存在时,直线l1的方程为x=0,
此时
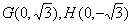 ,
,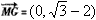 ,
,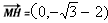 ,
,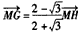
所以
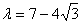
所以
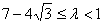 ,
,即所求λ的取值范围是
 。
。
练习册系列答案
相关题目
 如图,以椭圆
如图,以椭圆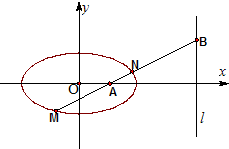 设椭圆C:
设椭圆C: (a>b>0)过点
(a>b>0)过点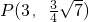 ,且离心率
,且离心率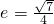 .
.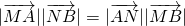 .
.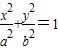 (a>b>0)过点
(a>b>0)过点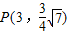 ,且离心率
,且离心率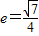 .
. .
.
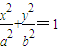 (a>b>0)过点
(a>b>0)过点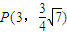 ,且离心率
,且离心率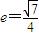 .
. .
.