题目内容
设椭圆C: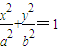 (a>b>0)过点
(a>b>0)过点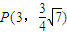 ,且离心率
,且离心率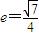 .
.(Ⅰ)求椭圆C的方程;
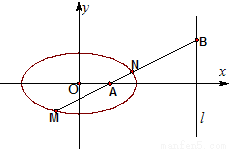
(Ⅱ)过点A(2,0)的动直线AB交椭圆于点M、N,(其中点N位于点A、B之间),且交直线l:x=8于点B(如图).证明:
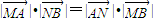 .
.
【答案】分析:(Ⅰ)由已知,得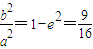 ,故可设所求椭圆方程为
,故可设所求椭圆方程为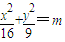 ,将点
,将点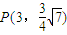 的坐标代入上式,得m=1.由此得到所求椭圆C的方程.
的坐标代入上式,得m=1.由此得到所求椭圆C的方程.
(Ⅱ)设M(x1,y1),N(x2,y2),要证原等式成立,只要证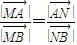 ?
?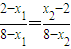 ?5(x1+x2)-x1x2=16.
?5(x1+x2)-x1x2=16.
解答:解:(Ⅰ) 由已知,得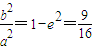 ,故可设所求椭圆方程为
,故可设所求椭圆方程为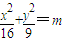 ,
,
将点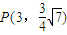 的坐标代入上式,得 m=1.
的坐标代入上式,得 m=1.
∴所求椭圆C的方程为: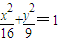 ;(5分)
;(5分)
(Ⅱ) 设M(x1,y1),N(x2,y2),
要证原等式成立,只要证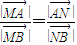 ?
?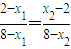 ?5(x1+x2)-x1x2=16.①(8分)
?5(x1+x2)-x1x2=16.①(8分)
以下证明①式成立.
证明:设MB:y=k(x-2),由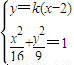 ⇒(9+16k2)x2-64k2x+64k2-144=0
⇒(9+16k2)x2-64k2x+64k2-144=0
由韦达定理,得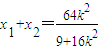 ,
,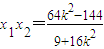 ,(11分)
,(11分)
∴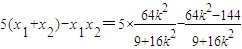 =
=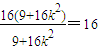
于是,①式得证.
∴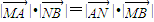 .(13分)
.(13分)
点评:本题考查椭圆方程的求法和证明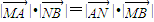 .解题时要认真审题,注意椭圆性质的合理运用和分析法证明的灵活运用.
.解题时要认真审题,注意椭圆性质的合理运用和分析法证明的灵活运用.
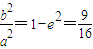 ,故可设所求椭圆方程为
,故可设所求椭圆方程为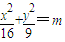 ,将点
,将点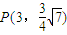 的坐标代入上式,得m=1.由此得到所求椭圆C的方程.
的坐标代入上式,得m=1.由此得到所求椭圆C的方程.(Ⅱ)设M(x1,y1),N(x2,y2),要证原等式成立,只要证
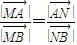 ?
?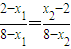 ?5(x1+x2)-x1x2=16.
?5(x1+x2)-x1x2=16.解答:解:(Ⅰ) 由已知,得
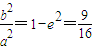 ,故可设所求椭圆方程为
,故可设所求椭圆方程为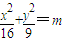 ,
,将点
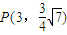 的坐标代入上式,得 m=1.
的坐标代入上式,得 m=1.∴所求椭圆C的方程为:
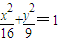 ;(5分)
;(5分)(Ⅱ) 设M(x1,y1),N(x2,y2),
要证原等式成立,只要证
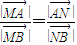 ?
?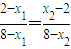 ?5(x1+x2)-x1x2=16.①(8分)
?5(x1+x2)-x1x2=16.①(8分)以下证明①式成立.
证明:设MB:y=k(x-2),由
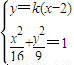 ⇒(9+16k2)x2-64k2x+64k2-144=0
⇒(9+16k2)x2-64k2x+64k2-144=0由韦达定理,得
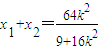 ,
,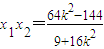 ,(11分)
,(11分)∴
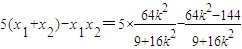 =
=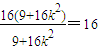
于是,①式得证.
∴
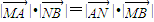 .(13分)
.(13分)点评:本题考查椭圆方程的求法和证明
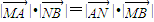 .解题时要认真审题,注意椭圆性质的合理运用和分析法证明的灵活运用.
.解题时要认真审题,注意椭圆性质的合理运用和分析法证明的灵活运用. 
练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
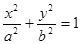 (a>b>0)的左、右焦点分别为F1、F2,P是C上的点,
(a>b>0)的左、右焦点分别为F1、F2,P是C上的点, ,
,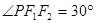 ,则C的离心率为( )
,则C的离心率为( )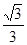 B.
B.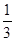 C.
C. D.
D.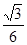
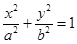 (a>b>0)过点(0,4),离心率为
(a>b>0)过点(0,4),离心率为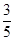
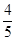 的直线被椭圆C所截线段的中点坐标。
的直线被椭圆C所截线段的中点坐标。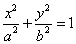 (a>b>0)过点(0,4),离心率为
(a>b>0)过点(0,4),离心率为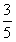 ,
,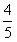 的直线被C所截线段的中点坐标。
的直线被C所截线段的中点坐标。 (a>b>0) 的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且
(a>b>0) 的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且 ,
,  相切,求椭圆C的方程:
相切,求椭圆C的方程: 
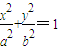 (a>b>0)的一个顶点坐标为A(
(a>b>0)的一个顶点坐标为A(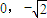 ),且其右焦点到直线
),且其右焦点到直线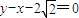 的距离为3.
的距离为3.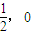 ),求证:点M的所有“相关弦”的中点在同一条直线上;
),求证:点M的所有“相关弦”的中点在同一条直线上;