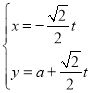题目内容
【题目】已知a≤8.函数f(x)=a1nx﹣x2+5,g(x)=2x+![]()
(1)若f(x)的极大值为5,求a的值
(2)若关于x的不等式f(x)≤g(x)在区间[1,+∞)上恒成立,求a的取值范围,(1n2≈0.7)
【答案】(1)a=2e;(2)![]()
【解析】
(1)求导后分![]() 的不同取值范围求
的不同取值范围求![]() 的最值,进而分析函数的极值再代入求解即可.
的最值,进而分析函数的极值再代入求解即可.
(2)构造函数![]() 再求导分析单调性,分情况讨论最大值再根据最大值
再求导分析单调性,分情况讨论最大值再根据最大值![]() 求关于参数a的取值范围即可.
求关于参数a的取值范围即可.
(1)函数f(x)=a1nx﹣x2+5,函数的定义域为{x|x>0},
函数的f(x)的导数f′(x)=![]() ﹣2x=
﹣2x=![]() ,
,
当a≤0,则f′(x)<0,此时函数单调递减无极大值,∴a>0,
∴f(x)在(0,![]() )上单调递增,在(
)上单调递增,在(![]() ,+∞)上函数单调递减,
,+∞)上函数单调递减,
函数f(x)的极大值为:f(![]() )=5,解得:a=2e;
)=5,解得:a=2e;
(2)关于x的不等式f(x)≤g(x)在区间[1,+∞)上恒成立,
即:a1nx﹣x2+5﹣2x﹣![]() ≤0在区间[1,+∞)上恒成立,
≤0在区间[1,+∞)上恒成立,
令为h(x)=a1nx﹣x2+5﹣2x﹣![]() ,x∈[1,+∞),
,x∈[1,+∞),
则有:h′(x)=![]() ﹣2x﹣2+
﹣2x﹣2+![]() =﹣
=﹣![]() ,
,
①当a≤2时,h′(x)≤0,h(x)在区间[1,+∞)上单调递减,
h(x)最大值=h(1)=2﹣a≤0,即:a≥2,∴a=2;
②当a>2时,h(x)在区间[1,![]() )上单调递增,在区间(
)上单调递增,在区间(![]() ,+∞)上单调递减,
,+∞)上单调递减,
h(x)最大值=h(![]() )=
)=![]() 1n
1n![]() ﹣
﹣![]() +5﹣2
+5﹣2![]() ≤0,
≤0,
令![]() =t∈(1,4],即:t1nt﹣t+5﹣4
=t∈(1,4],即:t1nt﹣t+5﹣4![]() ≤0,令u(t)=t1nt﹣t+5﹣4
≤0,令u(t)=t1nt﹣t+5﹣4![]() ,u′(t)=1nt﹣
,u′(t)=1nt﹣![]() ,
,
由u(t)在(1,4]上单调递增,且u′(1)<0,u′(4)>0,
知存在t0∈(1,4]使得且u′(t0)=0,
u(t)在区间(1,t0)上单调递减,在区间(t0,4]上单调递增,
又且u(1)=0,u(4)=41n4﹣7=8ln2﹣7<0,
∴t1nt﹣t+5﹣4![]() ≤0,在t∈(1,4]上恒成立,∵已知a≤8,故:2<a≤8,
≤0,在t∈(1,4]上恒成立,∵已知a≤8,故:2<a≤8,
即a的取值范围是:a∈![]()