题目内容
17.已知a>0,g(x)是函数f(x)=(x-a)lnx+$\frac{x-1}{ax}$的导函数.(Ⅰ)当a=1时,求函数g(x)的单调递减区间;
(Ⅱ)当a>1时,求证:函数g(x)在x∈[1,+∞)是单调递增函数;
(Ⅲ)若存在x0∈[1,+∞),使得不等式f(x0)<0成立,求实数a的取值范围.
分析 (I)a=1时,化简函数g(x),求出函数的导数,由g′(x)<0,求解可得函数g(x)的单调递减区间.
(II)求出函数的导数,通过a>1时,判断g′(x)≥g′(1)>0,恒成立,即可证明函数g(x)在x∈[1,+∞)是单调递增函数.
(III)当0<a≤1时,不存在x0∈[1,+∞),使得不等式f(x0)<0成立,当a>1时,函数f′(x)在x∈[1,+∞)是单调递增函数,讨论f′(1)≥0,f(x)≥f(1)≥0,推出不存在x0∈[1,+∞),使得不等式f(x0)<0成立;若f′(1)<0,推出f(x)≤f(1)=0,说明存在x0∈[1,m),使得不等式f(x0)<0,求解实数a的取值范围.
解答 解:(I)$g(x)=lnx+\frac{x-1}{x}+\frac{1}{x^2}$,$g'(x)=\frac{{{x^2}+x-2}}{x^3}$,…(2分)
由g′(x)<0得函数g(x)的单调递减区间是(0,1);…(4分)
(II)$g(x)=lnx+\frac{x-a}{x}+\frac{1}{{a{x^2}}}$,$g'(x)=\frac{{a{x^2}+{a^2}x-2}}{{a{x^3}}}$,
当a>1时,$g'(1)=\frac{(a+2)(a-1)}{{a{x^3}}}>0$,
∵二次函数y=ax2+a2x-2在x∈[1,+∞)是增函数,
∴g′(x)≥g′(1)>0,
∴函数g(x)在x∈[1,+∞)是单调递增函数;…(8分)
(III)当0<a≤1时,f′(x)>0,f(x)在x∈[1,+∞)是增函数,f(x)≥f(1)=0,
不存在x0∈[1,+∞),使得不等式f(x0)<0成立;…(10分)
当a>1时,函数f′(x)在x∈[1,+∞)是单调递增函数,
若f′(1)≥0,即$1<a≤\frac{{\sqrt{5}+1}}{2}$,
则f′(x)≥f′(1)≥0,f(x)在x∈[1,+∞)是增函数,f(x)≥f(1)≥0,
也不存在x0∈[1,+∞),使得不等式f(x0)<0成立;
若f′(1)<0,即$a>\frac{{\sqrt{5}+1}}{2}$,则存在m∈[1,+∞),
当x∈[1,m)时,f′(x)<0,f(x)在x∈[1,m)是减函数,f(x)≤f(1)=0
此时存在x0∈[1,m),使得不等式f(x0)<0成立,
综上,实数a的取值范围是$(\frac{{\sqrt{5}+1}}{2},+∞)$.…(12分)
点评 本题考查函数的导数的综合应用,函数的单调性的判断与应用,考查分析问题解决问题的能力.

| A. | 16 | B. | 20 | C. | 24 | D. | 32 |
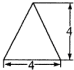 一个四棱锥的底面是正方形,其正视图和侧视图均为如图所示的等腰三角形,则该四棱锥的侧面积为16$\sqrt{5}$.
一个四棱锥的底面是正方形,其正视图和侧视图均为如图所示的等腰三角形,则该四棱锥的侧面积为16$\sqrt{5}$.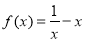 的图象关于( )
的图象关于( ) 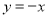 对称 C.
对称 C. 轴对称 D.直线
轴对称 D.直线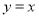 对称
对称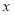 (吨)与相应的生产能耗
(吨)与相应的生产能耗 (吨标准煤)的几组对应数据,根据表中提供的数据,求出
(吨标准煤)的几组对应数据,根据表中提供的数据,求出 关于
关于 的线性回归方程
的线性回归方程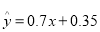 ,那么表中
,那么表中 的值为?( )
的值为?( )