题目内容
3.已知实数a1,a2,a3,a4各不相等,若集合{x|x=ai+aj,1≤i≤j}={1,2,3,5,6,7},则a12+a22+a32+a42=21.分析 令a1<a2<a3<a4,根据集合{x|x=ai+aj,1≤i≤j≤4}={1,2,3,4,5,6,7},可得实数a1,a2,a3,a4的值,进而得到答案.
解答 解:令a1<a2<a3<a4,
∵集合{x|x=ai+aj,1≤i≤j}={1,2,3,4,5,6,7},
令i=j=1,则2a1=1,解得a1=$\frac{1}{2}$,
令i=j=4,则2a4=7,解得a4=$\frac{7}{2}$,
令i=1,j=2,则a1+a2=2,解得a2=$\frac{3}{2}$,
令i=3,j=4,则a3+a4=6,解得a3=$\frac{5}{2}$,
则a12+a22+a32+a42=21,
故答案为:21.
点评 本题考查的知识点是集合相等,其中根据已知,求出实数a1,a2,a3,a4的值,是解答的关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
14.双曲线$\frac{x^2}{3}-\frac{y^2}{4}=1$的左焦点到右准线的距离为( )
| A. | $\frac{{3\sqrt{7}}}{7}$ | B. | $\frac{22}{5}$ | C. | $\frac{28}{5}$ | D. | $\frac{{10\sqrt{7}}}{7}$ |
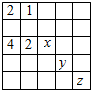 在如图所示的表格中,如果第一格填上一个数后,每一行成等比数列,每一列成等差数列,则x+y+z=2.
在如图所示的表格中,如果第一格填上一个数后,每一行成等比数列,每一列成等差数列,则x+y+z=2. (理科)如图,A,B,C,D在y=$\frac{1}{4}$x2上,A、D关于抛物线对称轴对称,过点D(x0,y0)作抛物线切线,可证切线斜率为$\frac{1}{2}$x0,BC∥切线,点D到AB,AC距离分别为d1,d2,d1+d2=$\sqrt{2}$|AD|
(理科)如图,A,B,C,D在y=$\frac{1}{4}$x2上,A、D关于抛物线对称轴对称,过点D(x0,y0)作抛物线切线,可证切线斜率为$\frac{1}{2}$x0,BC∥切线,点D到AB,AC距离分别为d1,d2,d1+d2=$\sqrt{2}$|AD|