题目内容
(本小题满分16分)
设函数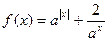 (其中常数
(其中常数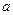 >0,且
>0,且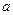 ≠1).
≠1).
(Ⅰ)当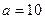 时,解关于
时,解关于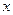 的方程
的方程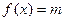 (其中常数
(其中常数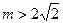 );
);
(Ⅱ)若函数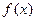 在
在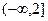 上的最小值是一个与
上的最小值是一个与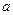 无关的常数,求实数
无关的常数,求实数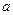 的取值范围.
的取值范围.
设函数
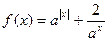 (其中常数
(其中常数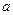 >0,且
>0,且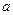 ≠1).
≠1).(Ⅰ)当
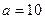 时,解关于
时,解关于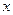 的方程
的方程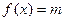 (其中常数
(其中常数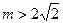 );
);(Ⅱ)若函数
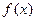 在
在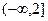 上的最小值是一个与
上的最小值是一个与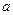 无关的常数,求实数
无关的常数,求实数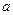 的取值范围.
的取值范围.(1)
当m>3时,方程f(x)=m有两解x=lg和x=lg;
当2<m≤3时,方程f(x)=m有两解x=lg
(2)当a≥
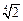 时,f(x)在(-∞,2]上的最小值与a无关
时,f(x)在(-∞,2]上的最小值与a无关解(Ⅰ)f(x)=
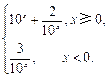
①当x<0时,f(x)=
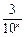 >3.因为m>2.则当2<m≤3时,方程f(x)=m无解;
>3.因为m>2.则当2<m≤3时,方程f(x)=m无解;当m>3,由10x=,得x=lg. …………………… 1分
②当x≥0时,10x≥1.由f(x)=m得10x+
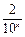 =m,∴(10x)2-m10x+2=0.
=m,∴(10x)2-m10x+2=0.因为m>2,判别式
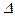 =m2-8>0,解得10x=.…………………… 3分
=m2-8>0,解得10x=.…………………… 3分因为m>2,所以>>1.所以由10x=,解得x=lg.
令=1,得m=3. …………………… 4分
所以当m>3时,=<=1,
当2<m≤3时,=>=1,
解得x=lg.…………… 5分
综上,当m>3时,方程f(x)=m有两解x=lg和x=lg;
当2<m≤3时,方程f(x)=m有两解x=lg.…………………… 6分
(2)
(Ⅰ)若0<a<1,当x<0时,0<f(x)=<3;当0≤x≤2时,f(x)=ax+.… 7分
令t=ax,则t∈[a2,1],g(t)=t+在[a2,1]上单调递减,所以当t=1,即x=0时f(x)取得最小值为3.
当t=a2时,f(x)取得最大值为
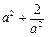 .此时f(x)在(-∞,2]上的值域是(0,
.此时f(x)在(-∞,2]上的值域是(0,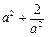 ],没有最小值.…………………… 9分
],没有最小值.…………………… 9分(Ⅱ)若a>1,当x<0时,f(x)=>3;当0≤x≤2时f(x)=ax+.
令t=ax,g(t)=t+,则t∈[1,a2].
①若a2≤
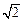 ,g(t)=t+在[1,a2]上单调递减,所以当t=a2即x=2时f(x)取最小值a2+,最小值与a有关;…………………………… 11分
,g(t)=t+在[1,a2]上单调递减,所以当t=a2即x=2时f(x)取最小值a2+,最小值与a有关;…………………………… 11分②a2≥
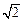 ,g(t)=t+在[1,]上单调递减,在[,a2]上单调递增,…………13分
,g(t)=t+在[1,]上单调递减,在[,a2]上单调递增,…………13分所以当t=即x=loga时f(x)取最小值2,最小值与a无关.……………… 15分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
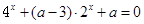 在
在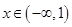 上有两个不等实根,则实数a的取值范围是 ( )
上有两个不等实根,则实数a的取值范围是 ( )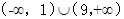
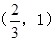
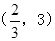
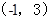
 ,深为3m,如果池底每平方米造价为80元,池壁每平方米造价为60元,问怎样设计水池能使总造价最低,最低总造价是多少元?
,深为3m,如果池底每平方米造价为80元,池壁每平方米造价为60元,问怎样设计水池能使总造价最低,最低总造价是多少元?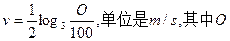 表示鱼的耗氧量的单位数,
表示鱼的耗氧量的单位数,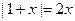 的根.
的根. 的函数
的函数
 ,若关于
,若关于 的方程
的方程 有三个不同的实数解
有三个不同的实数解 、
、 、
、 ,则
,则 ___________
___________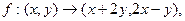 在影射
在影射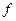 下(3,1)的原象为 ( )
下(3,1)的原象为 ( )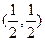
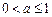 ,函数
,函数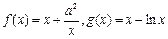 ,若对任意的
,若对任意的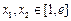 ,都有
,都有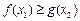 成立,则实数
成立,则实数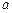 的取值范围为
的取值范围为