题目内容
(本题满分14分)
已知函数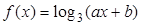 的图象经过点
的图象经过点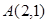 和
和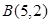 ,记
,记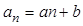 (
(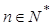 )
)
(1)求数列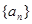 的通项公式;
的通项公式;
(2)设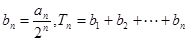 ,若
,若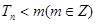 ,求
,求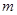 的最小值;
的最小值;
(3)求使不等式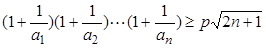 对一切
对一切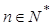 均成立的最大实数
均成立的最大实数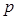 .
.
已知函数
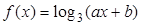 的图象经过点
的图象经过点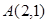 和
和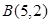 ,记
,记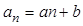 (
(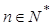 )
)(1)求数列
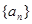 的通项公式;
的通项公式;(2)设
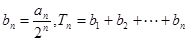 ,若
,若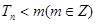 ,求
,求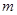 的最小值;
的最小值;(3)求使不等式
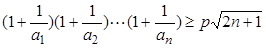 对一切
对一切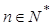 均成立的最大实数
均成立的最大实数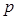 .
.(1)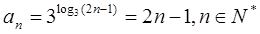 ;
;
(2)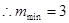 ; (3)
; (3) .
.
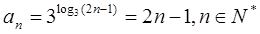 ;
;(2)
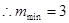 ; (3)
; (3) .
. 本试题主要是借助于函数为背景求解数列的通项公式,并利用错位相减法得到数列的和,同时利用放缩法得到不等式的证明。
(1)因为函数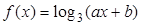 的图象经过点
的图象经过点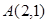 和
和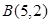 ,记
,记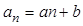 ,联立方程组得到a,b的值。
,联立方程组得到a,b的值。
(2)由(1)得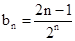 ,然后利用错位相减法得到数列的和。
,然后利用错位相减法得到数列的和。
(3)要使不等式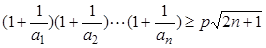 对一切
对一切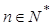 均成立,则可以分离参数p,得到关于n的表达式,进而求解数列的最值,得到参数p的范围。
均成立,则可以分离参数p,得到关于n的表达式,进而求解数列的最值,得到参数p的范围。
解:(1)由题意得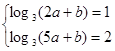 ,解得
,解得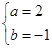 , …………2分
, …………2分
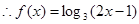
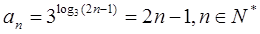 …………4分
…………4分
(2)由(1)得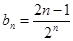 ,
, 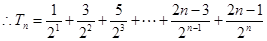 ①
①
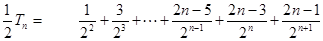 ② ①-②得
② ①-②得
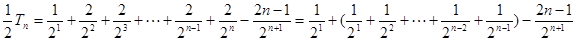
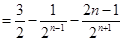 .
. 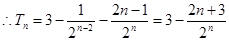 , …………7分
, …………7分
设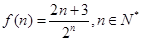 ,则由
,则由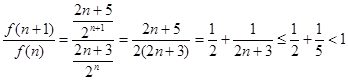
得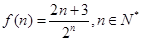 随
随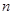 的增大而减小,
的增大而减小,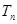 随
随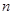 的增大而增大。
的增大而增大。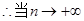 时,
时,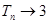
又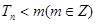 恒成立,
恒成立,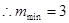 ………10分
………10分
(3)由题意得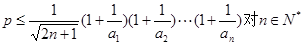 恒成立
恒成立
记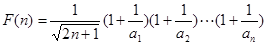 ,则
,则
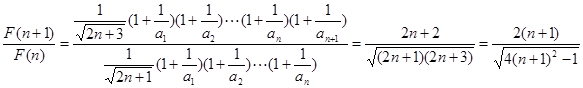
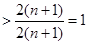 …………12分
…………12分
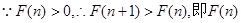 是随
是随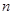 的增大而增大
的增大而增大
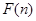 的最小值为
的最小值为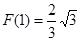 ,
,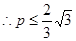 ,即
,即 . …………14分
. …………14分
(1)因为函数
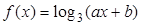 的图象经过点
的图象经过点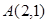 和
和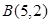 ,记
,记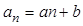 ,联立方程组得到a,b的值。
,联立方程组得到a,b的值。(2)由(1)得
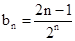 ,然后利用错位相减法得到数列的和。
,然后利用错位相减法得到数列的和。(3)要使不等式
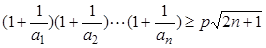 对一切
对一切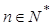 均成立,则可以分离参数p,得到关于n的表达式,进而求解数列的最值,得到参数p的范围。
均成立,则可以分离参数p,得到关于n的表达式,进而求解数列的最值,得到参数p的范围。解:(1)由题意得
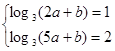 ,解得
,解得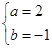 , …………2分
, …………2分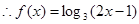
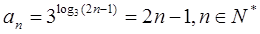 …………4分
…………4分(2)由(1)得
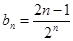 ,
, 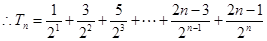 ①
①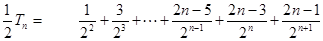 ② ①-②得
② ①-②得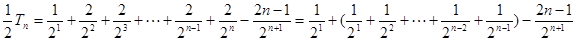
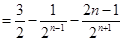 .
. 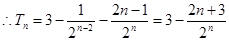 , …………7分
, …………7分设
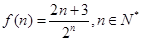 ,则由
,则由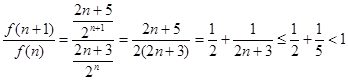
得
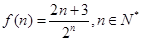 随
随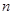 的增大而减小,
的增大而减小,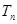 随
随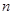 的增大而增大。
的增大而增大。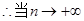 时,
时,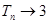
又
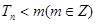 恒成立,
恒成立,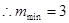 ………10分
………10分(3)由题意得
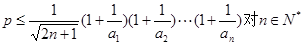 恒成立
恒成立记
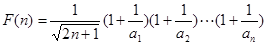 ,则
,则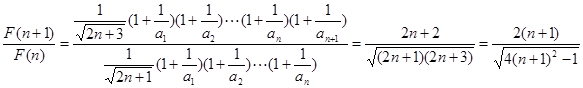
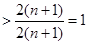 …………12分
…………12分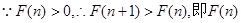 是随
是随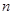 的增大而增大
的增大而增大 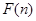 的最小值为
的最小值为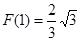 ,
,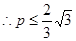 ,即
,即 . …………14分
. …………14分
练习册系列答案
相关题目
 ,则
,则 的值为( )
的值为( )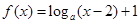
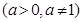 的图象恒过定点
的图象恒过定点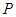 ,则
,则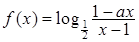 为奇函数,
为奇函数,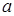 为常数。
为常数。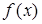 在区间
在区间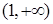 内单调递增;
内单调递增;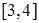 上的每一个
上的每一个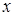 的值,不等式
的值,不等式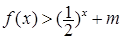 恒成立,求实数
恒成立,求实数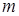 的取值范围。
的取值范围。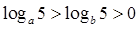 ,那么a、b间的关系是
,那么a、b间的关系是 



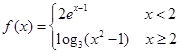 ,则不等式
,则不等式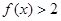 的解集为( )
的解集为( )

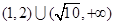

 ,则
,则 的值为 ( )
的值为 ( )

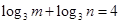 ,那么
,那么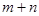 的最小值是 .
的最小值是 .