题目内容
设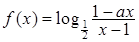 为奇函数,
为奇函数,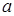 为常数。
为常数。
(I)求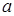 的值;
的值;
(II)证明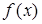 在区间
在区间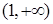 内单调递增;
内单调递增;
(III)若对于区间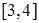 上的每一个
上的每一个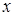 的值,不等式
的值,不等式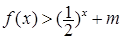 恒成立,求实数
恒成立,求实数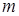 的取值范围。
的取值范围。
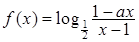 为奇函数,
为奇函数,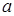 为常数。
为常数。(I)求
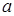 的值;
的值;(II)证明
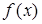 在区间
在区间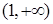 内单调递增;
内单调递增;(III)若对于区间
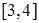 上的每一个
上的每一个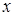 的值,不等式
的值,不等式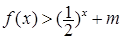 恒成立,求实数
恒成立,求实数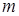 的取值范围。
的取值范围。(Ⅰ) 。(Ⅱ)略(III)
。(Ⅱ)略(III)
 。(Ⅱ)略(III)
。(Ⅱ)略(III)
(I)根据f(-x)+f(x)=0恒成立,可求得a值。
(II)根据复合函数的单调性在(I)知道a值的情况下,可以研究内函数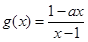 它在
它在 上是减函数即可。
上是减函数即可。
(III) 解本小题的关键是把原不等式转化为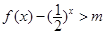 ,然后
,然后
令 ,则
,则 对于区间
对于区间 上的每一个
上的每一个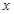 都成立进一步转化为
都成立进一步转化为 在
在 上的最小值大于
上的最小值大于
(II)根据复合函数的单调性在(I)知道a值的情况下,可以研究内函数
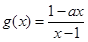 它在
它在 上是减函数即可。
上是减函数即可。(III) 解本小题的关键是把原不等式转化为
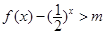 ,然后
,然后令
 ,则
,则 对于区间
对于区间 上的每一个
上的每一个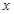 都成立进一步转化为
都成立进一步转化为 在
在 上的最小值大于
上的最小值大于

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 (log2 x)]=0,求x。;
(log2 x)]=0,求x。; ,求
,求 的值。
的值。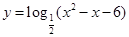 的单调递增区间是 .
的单调递增区间是 .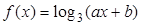 的图象经过点
的图象经过点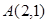 和
和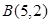 ,记
,记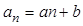 (
(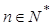 )
)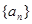 的通项公式;
的通项公式;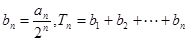 ,若
,若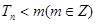 ,求
,求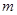 的最小值;
的最小值;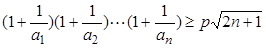 对一切
对一切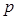 .
.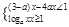 在区间
在区间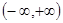 内是增函数,则
内是增函数,则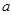 的取值范围是( )
的取值范围是( )


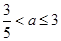
 ,则( )
,则( )



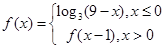 ,则f(3)的值为( )
,则f(3)的值为( ) 的定义域和值域都是
的定义域和值域都是 ,则
,则 =
= 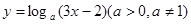 的图象过定点( )
的图象过定点( )


