题目内容
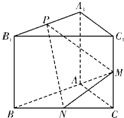 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N分别是
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N分别是CC1、BC的中点,点P在A1B1上,且满足
. |
| A1P |
. |
| A1B1 |
(1)证明:PN⊥AM;
(2)当λ取何值时,直线PN与平面ABC所成的角θ最大?并求该最大角的正切值;
(3)若平面PMN与平面ABC所成的二面角为45°,试确定点P的位置.
分析:(1)以AB,AC,AA1分别为x,y,z轴,建立空间直角坐标系A-xyz,求出各点的坐标及对应向量的坐标,易判断
•
=0,即PN⊥AM;
(2)设出平面ABC的一个法向量,我们易表达出sinθ,然后利用正弦函数的单调性及正切函数的单调性的关系,求出满足条件的λ值,进而求出此时θ的正线值;
(3)平面PMN与平面ABC所成的二面角为45°,则平面PMN与平面ABC法向量的夹角为45°,代入向量夹角公式,可以构造一个关于λ的方程,解方程即可求出对应λ值,进而确定出满足条件的点P的位置.
. |
| PN |
. |
| AM |
(2)设出平面ABC的一个法向量,我们易表达出sinθ,然后利用正弦函数的单调性及正切函数的单调性的关系,求出满足条件的λ值,进而求出此时θ的正线值;
(3)平面PMN与平面ABC所成的二面角为45°,则平面PMN与平面ABC法向量的夹角为45°,代入向量夹角公式,可以构造一个关于λ的方程,解方程即可求出对应λ值,进而确定出满足条件的点P的位置.
解答: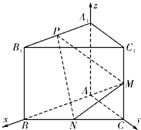 解:(1)证明:如图,以AB,AC,AA1分别为x,y,z轴,建立空间直角坐标系A-xyz.
解:(1)证明:如图,以AB,AC,AA1分别为x,y,z轴,建立空间直角坐标系A-xyz.
则P(λ,0,1),N(
,
,0),M(0,1,
),(2分)
从而
=(
-λ,
,-1),
=(0,1,
),
•
=(
-λ)×0+
×1-1×
=0,
所以PN⊥AM.(3分)
(2)平面ABC的一个法向量为
=(0,0,1),
则sinθ=|sin(
-<
,
>)|=|cos<
,
>|
=|
|=
(※).(5分)
而θ∈[0,
],当θ最大时,sinθ最大,tanθ最大,θ=
除外,
由(※)式,当λ=
时,(sinθ)max=
,(tanθ)max=2.(6分)
(3)平面ABC的一个法向量为
=
=(0,0,1).
设平面PMN的一个法向量为
=(x,y,z),
由(1)得
=(λ,-1,
).
由
得
解得
令x=3,得
=(3,2λ+1,2(1-λ))
∵平面PMN与平面ABC所成的二面角为45°,
∴|cos<
,
>|=|
|=
=
,
解得λ=-
.(11分)
故点P在B1A1的延长线上,且|A1P|=
.(12分)
 解:(1)证明:如图,以AB,AC,AA1分别为x,y,z轴,建立空间直角坐标系A-xyz.
解:(1)证明:如图,以AB,AC,AA1分别为x,y,z轴,建立空间直角坐标系A-xyz.则P(λ,0,1),N(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
从而
. |
| PN |
| 1 |
| 2 |
| 1 |
| 2 |
. |
| AM |
| 1 |
| 2 |
. |
| PN |
. |
| AM |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以PN⊥AM.(3分)
(2)平面ABC的一个法向量为
| n |
则sinθ=|sin(
| π |
| 2 |
. |
| PN |
| n |
. |
| PN |
| n |
=|
| ||||||
|
| 1 | ||||||
|
而θ∈[0,
| π |
| 2 |
| π |
| 2 |
由(※)式,当λ=
| 1 |
| 2 |
2
| ||
| 5 |
(3)平面ABC的一个法向量为
| n |
. |
| AA 1 |
设平面PMN的一个法向量为
| m |
由(1)得
. |
| MP |
| 1 |
| 2 |
由
|
|
解得
|
| m |
∵平面PMN与平面ABC所成的二面角为45°,
∴|cos<
| m |
| n |
| ||||
|
|
| |2(1-λ)| | ||
|
| ||
| 2 |
解得λ=-
| 1 |
| 2 |
故点P在B1A1的延长线上,且|A1P|=
| 1 |
| 2 |
点评:本题考查的知识点是向量评议表述线线的垂直、平等关系,用空间向量求直线与平面的夹角,用空间向量求平面间的夹角,其中熟练掌握向量夹角公式是解答此类问题的关键.

练习册系列答案
相关题目
 如图,已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC=BC=2,AA1=4,
如图,已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC=BC=2,AA1=4, 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,且AB⊥AC,M是CC1的中点,N是BC的中点,点P在直线A1B1上,且满足
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,且AB⊥AC,M是CC1的中点,N是BC的中点,点P在直线A1B1上,且满足 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别是CC1,BC的中点,点P在直线A1B1上,且
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别是CC1,BC的中点,点P在直线A1B1上,且 如图,已知三棱柱ABC-A1B1C1的所有棱长均为2,且A1A⊥底面ABC,D为AB的中点,G为△ABC1的重心,则|
如图,已知三棱柱ABC-A1B1C1的所有棱长均为2,且A1A⊥底面ABC,D为AB的中点,G为△ABC1的重心,则| 如图,已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=BC,∠ABC=90°,D为AC中点.
如图,已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=BC,∠ABC=90°,D为AC中点.