题目内容
8.已知六边形ABCDEF的三对对边都互相平行,并且$\overrightarrow{FC}$=2$\overrightarrow{AB}$=2$\overrightarrow{DE}$,又设$\overrightarrow{AB}$=$\overrightarrow{α}$,$\overrightarrow{BC}$=$\overrightarrow{β}$,求$\overrightarrow{CE}$和$\overrightarrow{CD}$.分析 画出六边形,根据条件知AB∥DE,且AB=DE,且AB∥FC,FC=2AB,从而四边形ABDE为平行四边形,连接对角线,交点O应在FC上.结合图形即可看出:$\overrightarrow{OE}=\overrightarrow{BO}=\overrightarrow{BA}+\overrightarrow{BC}$,$\overrightarrow{CO}=\overrightarrow{BA}$,从而可以得出$\overrightarrow{CE}=-2\overrightarrow{α}+\overrightarrow{β}$,而由$\overrightarrow{CE}+\overrightarrow{ED}$即可表示出$\overrightarrow{CD}$.
解答 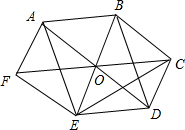 解:如图,根据$\overrightarrow{FC}=2\overrightarrow{AB}=2\overrightarrow{DE}$知,AB∥DE,AB=DE,AB∥FC,FC=2AB;
解:如图,根据$\overrightarrow{FC}=2\overrightarrow{AB}=2\overrightarrow{DE}$知,AB∥DE,AB=DE,AB∥FC,FC=2AB;
∴四边形ABDE为平行四边形,连接AD,BE,设交于O;
则O点在线段FC上;
∴$\overrightarrow{OE}=\overrightarrow{BO}=\overrightarrow{BA}+\overrightarrow{BC}$,$\overrightarrow{CO}=\overrightarrow{BA}$;
∴$\overrightarrow{CE}=\overrightarrow{CO}+\overrightarrow{OE}=\overrightarrow{BA}+\overrightarrow{BA}+\overrightarrow{BC}$=$-2\overrightarrow{AB}+\overrightarrow{BC}=-2\overrightarrow{α}+\overrightarrow{β}$;
∴$\overrightarrow{CD}=\overrightarrow{CE}+\overrightarrow{ED}=-2\overrightarrow{α}+\overrightarrow{β}+\overrightarrow{α}$=$-\overrightarrow{α}+\overrightarrow{β}$.
点评 考查向量相等的概念,向量数乘的几何意义,平行四边形的定义,平行四边形的对角线互相平分,以及向量加法的平行四边形法则,向量加法的几何意义.

 学习实践园地系列答案
学习实践园地系列答案| 房价(元) | 住房率(%) |
| 160 | 55 |
| 140 | 65 |
| 120 | 75 |
| 100 | 85 |