Question

【题目】定义域为R的偶函数f（x）满足对x∈R，有f（x+2）=f（x）﹣f（1），且当x∈[2，3]时，f（x）=﹣2x2+12x﹣18，若函数y=f（x）﹣loga（|x|+1）在（0，+∞）上至少有三个零点，则a的取值范围是（ ）
A.
B.
C.
D.

Answer 1

【答案】A
【解析】解：因为 f（x+2）=f（x）﹣f（1），且f（x）是定义域为R的偶函数

令x=﹣1 所以 f（﹣1+2）=f（﹣1）﹣f（1），f（﹣1）=f（1）

即 f（1）=0 则有，f（x+2）=f（x）

f（x）是周期为2的偶函数，

当x∈[2，3]时，f（x）=﹣2x2+12x﹣18=﹣2（x﹣3）2

图象为开口向下，顶点为（3，0）的抛物线

∵函数y=f（x）﹣loga（|x|+1）在（0，+∞）上至少有三个零点，

∵f（x）≤0，

∴g（x）≤0，可得a＜1，

要使函数y=f（x）﹣loga（|x|+1）在（0，+∞）上至少有三个零点，

令g（x）=loga（|x|+1），

如图要求g（2）＞f（2），可得

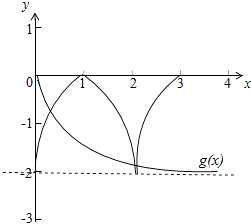
就必须有 loga（2+1）＞f（2）=﹣2，

∴可得loga3＞﹣2，∴3＜ ，解得﹣ ＜a＜ 又a＞0，

∴0＜a＜ ，

故选A；

根据定义域为R的偶函数f（x）满足对x∈R，有f（x+2）=f（x）﹣f（1），可以令x=﹣1，求出f（1），再求出函数f（x）的周期为2，当x∈[2，3]时，f（x）=﹣2x2+12x﹣18，画出图形，根据函数y=f（x）﹣loga（|x|+1）在（0，+∞）上至少有三个零点，利用数形结合的方法进行求解；