题目内容
已知椭圆 的一个顶点为B(0,4),离心率
的一个顶点为B(0,4),离心率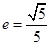 , 直线
, 直线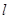 交椭圆于M,N两点.
交椭圆于M,N两点.
(1)若直线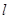 的方程为y=x-4,求弦MN的长:
的方程为y=x-4,求弦MN的长:
(2)如果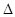 BMN的重心恰好为椭圆的右焦点F,求直线
BMN的重心恰好为椭圆的右焦点F,求直线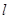 的方程.
的方程.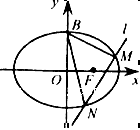
 的一个顶点为B(0,4),离心率
的一个顶点为B(0,4),离心率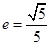 , 直线
, 直线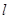 交椭圆于M,N两点.
交椭圆于M,N两点.(1)若直线
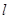 的方程为y=x-4,求弦MN的长:
的方程为y=x-4,求弦MN的长:(2)如果
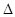 BMN的重心恰好为椭圆的右焦点F,求直线
BMN的重心恰好为椭圆的右焦点F,求直线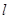 的方程.
的方程.
(1)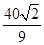 ;(2)
;(2)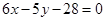 .
.
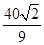 ;(2)
;(2)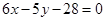 .
.试题分析:(1)由椭圆顶点
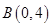 知
知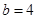 ,又离心率
,又离心率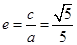 ,且
,且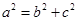 ,所以
,所以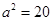 ,从而求得椭圆方程为
,从而求得椭圆方程为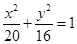 ,联立椭圆方程与直线
,联立椭圆方程与直线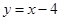 消去
消去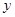 得
得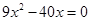 ,
,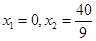 ,再根据弦长公式
,再根据弦长公式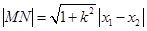 ,可求得弦
,可求得弦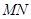 的长;(2)由题意可设线段
的长;(2)由题意可设线段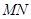 的中点为
的中点为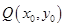 ,则根据三角形重心的性质知
,则根据三角形重心的性质知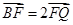 ,可求得
,可求得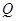 的坐标为
的坐标为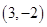 ,又设直线
,又设直线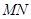 的方程为
的方程为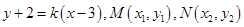 ,根据中点公式得
,根据中点公式得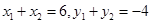 ,又由点
,又由点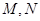 是椭圆上的点所以
是椭圆上的点所以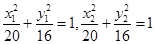 ,两式相减整理得
,两式相减整理得 ,从而可求出直线
,从而可求出直线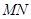 的方程.
的方程.(1)由已知
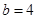 ,且
,且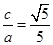 ,
,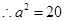 .所以椭圆方程为
.所以椭圆方程为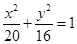 . 4分
. 4分由
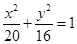 与
与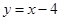 联立,消去
联立,消去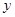 得
得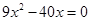 ,
,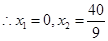 . 6分
. 6分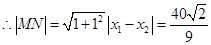 . 7分
. 7分(2)椭圆右焦点
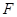 的坐标为
的坐标为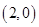 ,设线段
,设线段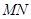 的中点为
的中点为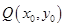 ,由三角形重心的性质知
,由三角形重心的性质知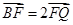 ,又
,又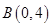 ,
,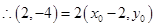 ,故得
,故得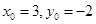 .所以得
.所以得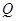 的坐标为
的坐标为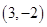 . 9分
. 9分设直线
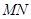 的方程为
的方程为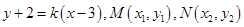 ,则
,则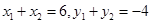 ,且
,且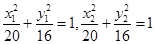 ,两式相减得
,两式相减得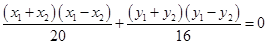 . 11分
. 11分 ,故直线
,故直线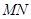 的方程为
的方程为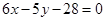 . 13分
. 13分

练习册系列答案
相关题目
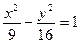 的一个顶点和一个焦点,圆心在此双曲线上,则圆心到双曲线中心的距离为( )
的一个顶点和一个焦点,圆心在此双曲线上,则圆心到双曲线中心的距离为( ) 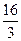
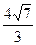
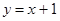 的倾斜角为( )
的倾斜角为( )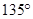
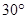
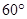
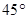

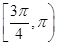

 ∪
∪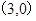 和点
和点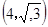 的直线的倾斜角是( )
的直线的倾斜角是( )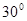
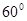
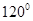
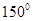
 的倾斜角为钝角,则实数
的倾斜角为钝角,则实数 的取值范围是 .
的取值范围是 .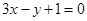 的斜率是( )
的斜率是( )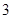

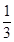
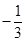
 和
和 的直线
的直线 的斜率为 .
的斜率为 .